Định lý pitago là một trong những kiến thức quan trọng nhất của hình học cơ bản mà bất kỳ học sinh nào cũng cần phải nắm chắc. Chúng ta cùng tìm hiểu về định lý Pytago ngay sau đây nhé.
MỤC LỤC
Định lý Pytago (hay còn gọi là định lý Pythagoras theo tiếng Anh) là một liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý pitago thuận phát biểu rằng trong 1 tam giác vuông bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông. Định lý có thể viết thành một phương trình liên hệ giữa độ dài của các cạnh là a, b và c, thường gọi là công thức Pytago: \(c^2=a^2+b^2\) (trong đó c độ dài là cạnh huyền, a,b lần lượt là độ dài 2 cạnh góc vuông). Ngoài ra, định lý pitago là một trong 17 phương trình thay đổi thế giới
Như vậy trong bất kì 1 tam giác vuông nào thì bình phương cạnh huyền cũng sẽ bằng tổng bình phương hai cạnh góc vuông.
Theo định lý cho biết, cạnh góc vuông của tam giác kí hiệu là a và b, còn cạnh huyền kí hiệu là c của tam giác vuông đó. Ta luôn có phương trình của định lý Pitago như sau:
\(a^2+b^2=c^2\) (với c là độ dài cạnh huyền và a và b là độ dài hai cạnh góc vuông hay còn gọi là cạnh kề.)
Từ đó ta có công thức tính cạnh huyền tam giác vuông như sau: c=√(a²+b²) với c là cạnh huyền và a, b là độ dài 2 cạnh tam giác vuông
.jpg)
Ta có thể chứng minh định lý Pytago đơn giản qua hình dưới đây:
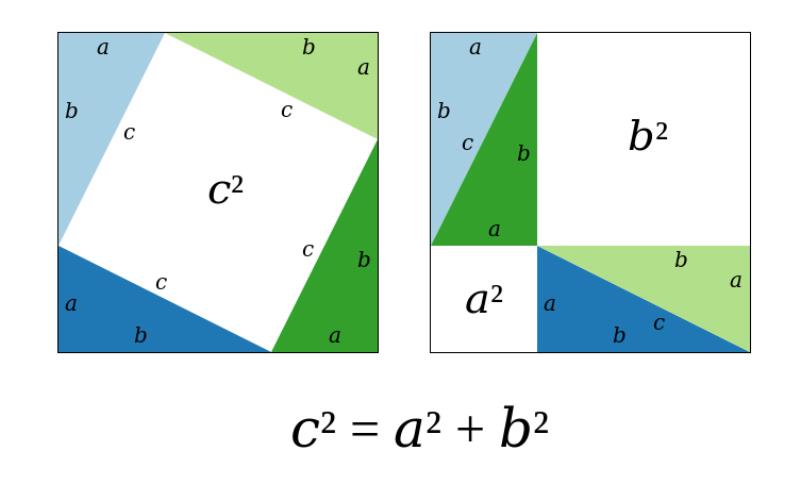
Ở hình trên ta có 2 hình vuông lớn có diện tích bằng nhau là: (a+b)^2
Trong mỗi hình lại có 4 tam giác vuông bằng nhau có diện băng nhau là 1/2(a.b). Do đó diện tích khoảng trắng của 2 hình sẽ bằng nhau.
Như vậy, diện tích của hình vuông c sẽ bằng tổng diện tích của 2 hình vuông a và b nên ta có: \(c^2=a^2+b^2\)
Xem thêm: Định Lý VI-ET (Viète) và Những Điều Cần Phải Biết
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.
Ví dụ: Tam giác ABC có \(BC^2=AB^2+AC^2\) => \(\widehat{BAC}\)= \(90^o\)
Định lý Pytago đảo được sử dụng rất phổ biến cũng như gồm nhiều ứng dụng trong thực tiễn. Đây là một định lý toán học quan trọng hàng đầu của hình học cơ bản.
Xem thêm: Tổng hợp công thức tính chu vi, diện tích hình thang
Gọi ABC là tam giác với các cạnh a, b, và c, với \(a^2+b^2=c^2\). Dựng một tam giác thứ hai có các cạnh bằng a và b và góc vuông tạo bởi giữa chúng. Theo định lý Pytago thuận, cạnh huyền của tam giác vuông thứ hai này sẽ bằng c=√(a²+b²) và bằng với cạnh còn lại của tam giác thứ nhất. Bởi vì cả hai tam giác có ba cạnh tương ứng cùng bằng chiều dài a, b và c, do vậy hai tam giác này phải bằng nhau. Do đó góc giữa các cạnh a và b ở tam giác đầu tiên phải là góc vuông.
Chứng minh định lý pytago đảo ở trên sử dụng chính định lý Pytago. Cũng có thể chứng minh định lý đảo mà không cần sử dụng tới định lý thuận.
Một hệ quả của định lý Pytago đảo đó là cách xác định đơn giản một tam giác có là tam giác vuông hay không, hay nó là tam giác nhọn hoặc tam giác tù. Gọi c là cạnh dài nhất của tam giác và có a + b > c (nếu không sẽ không tồn tại tam giác vì đây chính là bất đẳng thức tam giác). Các phát biểu sau đây là đúng:
Xem thêm: Học cách giải phương trình bậc 3 mà học sinh nào cũng phải biết
Khi học định lý Pitago, để nắm chắc và áp dụng tốt trong quá trình làm và giải các bài tập, bạn cần lưu ý các điều sau:
* Cạnh huyền của tam giác vuông luôn:
* Khi tính, bạn cần phải kiểm tra lại kết quả.
* Nhìn vào hình, bạn sẽ biết đâu là cạnh huyền vì đó là cạnh dài nhất đối diện góc lớn nhất. Còn cạnh ngắn nhất sẽ đối diện góc nhỏ nhất của tam giác.
* Ta chỉ tính được cạnh thứ 3 khi biết độ dài 2 cạnh còn lại trong tam giác vuông
* Nếu tam giác không phải là tam giác vuông, ta không thể áp dụng định lý pitago mà sẽ tính được khi biết thêm thông tin ngoài chiều dài 2 cạnh.
* Bạn nên vẽ tam giác để dễ dàng gán giá trị chính xác cho các cạnh a, b và c. Đặc biệt, các bài toán từ và toán logic áp dụng nhiều hơn cả.
* Nếu chỉ biết số đo một cạnh, ta không thể dùng định lý pitago để tính mà sẽ phải dùng hàm lượng giác (sin, cos, tan) hoặc tỉ lệ 30-60-90 / 45-45-90.
Đây là những lưu ý quan trọng để bạn có thể sử dụng định lý một cách linh hoạt cũng như trong những điều kiện nào thì không thể áp dụng được.
Sau đây là cách sử dụng định lý Pitago để chúng ta cùng tham khảo để áp dụng vào làm bài tập và thực tế.
Dựa theo định lý Pitago, ta sẽ cùng đi tìm các cạnh của tam giác vuông theo các bước sau:
Bước 1: Điều kiện tam giác đang xét phải là tam giác vuông
Định lý Pitago chỉ áp dụng được cho trường hợp tam giác vuông. Vì vậy, để tìm được các cạnh của tam giác vuông, hình tam giác đó phải có điều kiện là tam giác vuông với một góc bằng 90 độ. Bạn có thể tìm thấy dấu hiệu hình tam giác vuông trên hình vẽ rất dễ dàng.
Bước 2: Chỉ ra được các cạnh của hình tam giác vuông
Nhìn vào hình, bạn hãy chỉ ra 2 cạnh góc vuông và cạnh huyền. Cạnh luôn đối diện với góc vuông, là cạnh dài nhất sẽ là cạnh huyền. Hai cạnh ngắn hơn sẽ mặc định là 2 cạnh góc vuông. Ví dụ nếu tam giác ABC có cạnh góc vuông là ABC thì cạnh góc vuông là cạnh AB và BC còn cạnh huyền là AC. Theo định lý Pitago, a, b là kí hiệu của 2 cạnh góc vuông, c là kí hiệu của cạnh huyền.
Bước 3: Xác định cạnh huyền cần tìm của tam giác vuông đó
Với định lý Pitago, ta có thể tìm được độ dài bất kỳ của cạnh của một tam giác vuông nào bằng công thức trên chỉ cần biết chiều dài 2 cạnh còn lại: \(a^2+b^2=c^2\). Có nghĩa là bạn sẽ xác định cạnh chưa biết là a, b hay c. Nếu đã biết độ dài của 2 cạnh và 1 cạnh chưa biết của hình tam giác, bạn có thể bắt đầu.
Ví dụ: Nếu bạn đã biết cạnh huyền và một trong các cạnh bên còn lại sẽ dễ dàng tính được cạnh thứ 3 theo công thức ở trên.
Nếu có hai cạnh chưa biết độ dài, bạn cần xác định một cạnh nữa mới có thể sử dụng định lý Pitago. Bạn sẽ dùng các hàm lượng giác cơ bản để tìm độ dài của một cạnh nữa nếu biết số đo của một góc nhọn trong tam giác đó.
Bước 4: Thay giá trị độ dài 2 cạnh vào phương trình \(a^2+b^2=c^2\)
Trong đó, a, b là hai cạnh góc vuông, c là cạnh huyền. Nếu a = 3, c = 5 ta có \(3^2 + b^2 = 5^2\)
Bước 5: Tính bình phương
Giải phương trình, bạn tính bình phương mỗi cạnh đã biết. Nếu đơn giản, bạn để ở dạng số mũ rồi tính sau. Trong ví dụ này, bình phương lên ta được 9 + \(b^2\) = 25
Bước 6: Tách biến chưa biết sang một vế của phương trình
Nếu tính từng bước chi tiết, bạn sử dụng phép toán tính số hạng của tổng để chuyển hai số đã biết sang một bên của phương trình và số chưa biết ở một bên phương trình. Lúc này, cạnh huyền c đã ở một vế riêng để bạn tính hiệu số. => \(b^2\) = 16
Bước 7: Giảm bình phương của cả hai vế phương trình
Kết quả \(b^2\) = 16 cho thấy một vế của phương trình còn một biến bình phương còn vế kia là một số xác định. Giảm bình phương của cả 2 vế ta sẽ được b = 4. Như vậy kết quả của bài toán là 4, chiều dài số đo của cạnh cần tìm.
Bước 8: Sử dụng định lý Pitago để tìm cạnh của tam giác vuông trong thực tế
Định lý Pitago được sử dụng rất nhiều trong thực tế. Vì vậy, bạn chỉ cần nhận biết tam giác vuông trong thực tế trong bất kỳ trường hợp nào. Áp dụng vào thực tế cuộc sống, chỉ cần 2 đường thẳng giao nhau hoặc 2 vật giao nhau tạo ra một góc vuông đồng thời có một đường thẳng hay vật thứ 3 cắt chéo qua góc vuông đã tạo ra một hình tam giác vuông. Từ đó, bạn có thể sử dụng định lý pitago tìm độ dài cạnh nào đó khi biết số đo 2 cạnh còn lại.
Khi đã biết 2 tọa độ (x,y) là (6, 1), (3, 5), ta sẽ tính khoảng cách giữa 2 điểm trong mặt phẳng X-Y theo các bước sau:
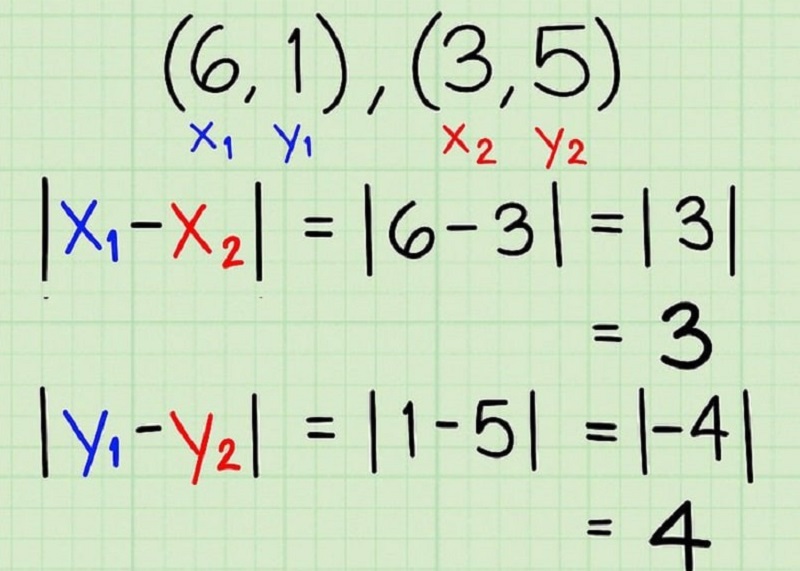
Bước 1: Xác định 2 điểm trong mặt phẳng X-Y
Dựa vào định lý Pitago, ta dễ dàng tính được khoảng cách đường thẳng giữa 2 điểm trong mặt phẳng X-Y. Lúc này, ta chỉ cần biết tọa độ x và y của 2 điểm bất kỳ. Bình thường tọa độ x, y sẽ được viết theo cặp thứ tự là tọa độ (x,y)
Muốn tìm khoảng cách giữa 2 điểm này, ta coi mỗi điểm là một trong những góc nhọn của tam giác vuông để thực hiện tính số đo chiều dài cạnh a, cạnh b sau đó tính tiếp độ dài cạnh c là khoảng cách giữa 2 điểm.
Bước 2: Vẽ 2 điểm trên đồ thị
Tọa độ (x, y) trên mặt phẳng X-Y, trong đó x là tọa độ trên trục hoành, y là tọa độ trên trục tung. Từ đó, bạn có thể tìm khoảng cách giữa 2 điểm mà không cần vẽ đồ thị. Vẽ đồ thị ra, hình vẽ sẽ giúp ta nhìn trực quan và rõ ràng hơn rất nhiều.
Bước 3: Tìm độ dài các cạnh góc vuông của tam giác
Dùng 2 điểm đã cho như các góc của tam giác ngay cạnh huyền, tìm độ dài cạnh góc vuông a và b. Bạn có thể tính qua hình trên đồ thị hoặc dùng công thức tính |x1 – x2| = |3 - 6| = |-3 | = 3
Chiều dài cạnh thẳng đứng tính như sau: |y1 - y2| = |1 - 5| = |-4 | = 4
Như vậy, hai cạnh còn lại của tam giác vuông này là a = 3, b = 4.
Bước 4: Dùng định lý pitago giải phương trình tìm cạnh huyền

Ở ví dụ ở trên, ta biết cạnh huyền là khoảng cách giữa 2 điểm của hình tam giác và tìm được 2 cạnh góc vuông còn lại ở trên. Bây giờ, chúng ta tìm cạnh huyền khi biết độ dài 2 cạnh góc vuông mà ta đặt là cạnh a và cạnh b.
Ở ví dụ trên, các điểm tọa độ (x, y) được cho là (3,5) và (6,1) và cho biết chiều dài 2 cạnh góc vuông là 3 và 4 để tính chiều dài cạnh huyền còn lại. Ta thực hiện cách tính chiều dài cạnh huyền bằng cách thay cạnh có chiều dài đã biết vào phương trình ta được: (3)²+(4)²= c² => c = 9+16 = 25 => c = 5. Như vậy, kết quả cuối cùng của phép tính độ dài là 5 về khoảng cách giữa hai điểm tạo độ (3,5) và (6,1).
Trên đây là những nội dung về định lý Pitago với dẫn chứng cụ thể, vieclam123.vn hy vọng sẽ giúp người học có thể hiểu chắc định lý cũng như áp dụng thành thạo vào làm bài tập liên quan.
>> Tham khảo thêm:
MỤC LỤC




Chia sẻ