Công thức tính chu vi, diện tích hình thang chuẩn nhất

Công thức tính diện tích hình thang, chu vi hình thang là một trong những kiến thức cơ bản nhất ta chúng ta được học ngay từ những năm đầu tiên tiếp xúc với toán hình. Tuy nhiên, sau một thời gian dài không sử dụng, chúng ta rất dễ nhầm lẫn với các công thức khác. Ở bài viết dưới đây, tôi xin sơ lược lại đôi nét về các kiến thức cơ bản về hình thang cũng như các công thức tính diện tích, chu vi hình thang cơ bản của hình này để các bạn tham khảo.

MỤC LỤC

1. Những kiến thức cơ bản về hình thang

Trước khi đi sâu vào nghiên cứu về công thức tính diện tích, chu vi hình thang, chúng ta cần biết hình thang được định nghĩa như thế nào? Theo định nghĩa trong sách toán học hình thang là một hình tứ giác lồi có hai cạnh song song nhau.

Hình thang có 3 loại thường gặp dưới đây:

Hình thang thường là tứ giác lồi có 2 cạnh song song với nhau.

Hình thang vuông sẽ có hai góc vuông, có chiều cao đồng thời là cạnh bên vuông góc với hai cạnh đáy. (Vd: Hình thang vuông ABCE có chiều cao là cạnh AE đồng thời là cạnh bên)

Hình thang cân là hình có hai cạnh bên bằng nhau, hai góc tạo bởi cạnh bên và cạnh đáy bằng nhau. (VD: Hình thang cân ABCD có 2 cạnh bên AD, BC bằng nhau và 2 góc ở đỉnh D và C bằng nhau)

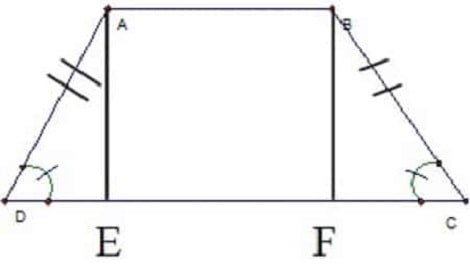
Nhìn chung việc nhận biết hình thang khá đơn giản và không gặp quá nhiều khó khăn.

2. Công thức tính diện tích hình thang cơ bản

Cũng giống như các đa giác khác, diện tích của hình thang là khoảng mặt phẳng được giới hạn bởi các cạnh của hình thang. Công thức này không quá phức tạp và tương đối dễ học.

Công thức tính diện tích hình thang bằng trung bình cộng của 2 đáy nhân với chiều cao của nó. \(S = \frac{1}{2} (a+b) h\) Trong đó S là diện tích, a,b là độ dài 2 đáy, h là chiều cao hình thang.

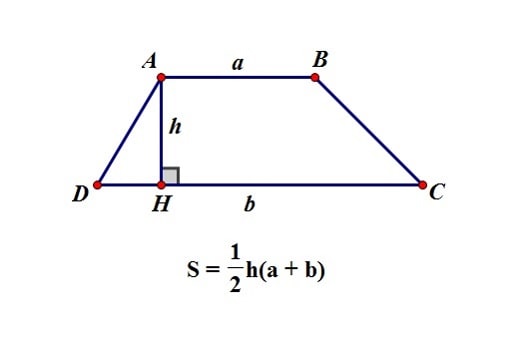
Cho a,b là độ dài 2 cạnh đáy của của hình thang ABCD, h là độ dài đường cao kẻ từ đỉnh A xuống cạnh đáy CD. Khi đó ta có công thức tính diện tích hình thang như sau:

\(S=\frac{1}{2}(a+b)h\)

Có thể phát biểu bằng lời như sau: Công thức tính diện tích hình thang bằng một phần hai của tổng hai cạnh đáy nhân với chiều cao

Đây là một dạng công thức tính diện tích của hình thang phổ biến nhất khi bạn làm các dạng bài tập công thức tính diện tích của hình thang.

Bạn có thể ghi nhớ công thức diện tích hình thang qua bài thơ sau:

Muốn tính diện tích hình thang

Đáy lớn đáy nhỏ ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi lấy nửa thế nào cũng ra

3. Công thức tính diện tích hình thang vuông

Công thức tính diện tích hình thang vương bằng trung bình cộng 2 đáy nhân với độ dài cạnh goc vuông. Công thức tính diện tích của hình thang vuông có công thức như sau:

\(S=\frac{a+b}{2}.h\)

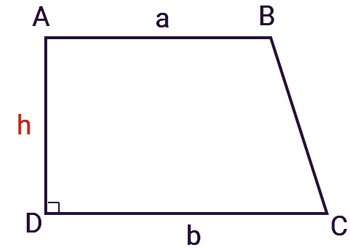
Cho hình thang vuông ABCD có cạnh bên AD đồng thời là đường cao kẻ từ A xuống cạnh CD. Độ dài hai cạnh đáy của hình thang lần lượt là a,b.

Khi đó diện tích của hình thang vuông là :

S=1/2 x (a+b) x h = 1/2x(AB+CD)xAD

4. Công thức tính diện tích hình thang cân

Để tính diện tích hình thang cân bạn có thể áp dụng công thức như hình thang thường hoặc chia hình thang cân thành 3 hình nhỏ gồm 1 hình chữ nhật và 2 hình tâm giác vuông bằng nhau để tính diện tích rồi cộng lại với nhau.

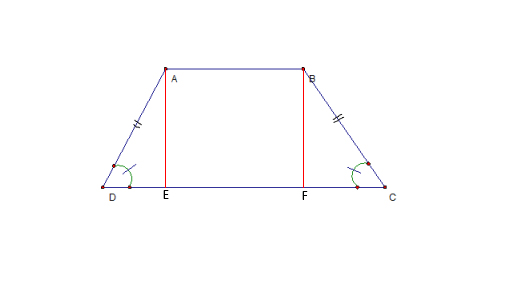
VD: SABCD = SABFE + SAED + SBCF

Mà SAED và SBCF Bằng nhau do 2 tam giác bằng nhau. (Ta có thể chứng minh được)

=> SABCD = SABFE + SAED + SBCF = SABFE + 2.SAED = AB*AE + AE*DE

5. Công thức tính diện tích hình thang khi biết bốn cạnh

Thông thường, chúng ta sẽ sử dụng công thức tính cần 3 yếu tố chính là độ dài hai cạnh đáy và chiều cao. Ở một số dạng bài tập nâng cao hơn, chúng ta sẽ được làm quen dần với công thức tính diện tích hình thang khi biết diện tích bốn cạnh. Bạn có thể hiểu công thức này như sau.

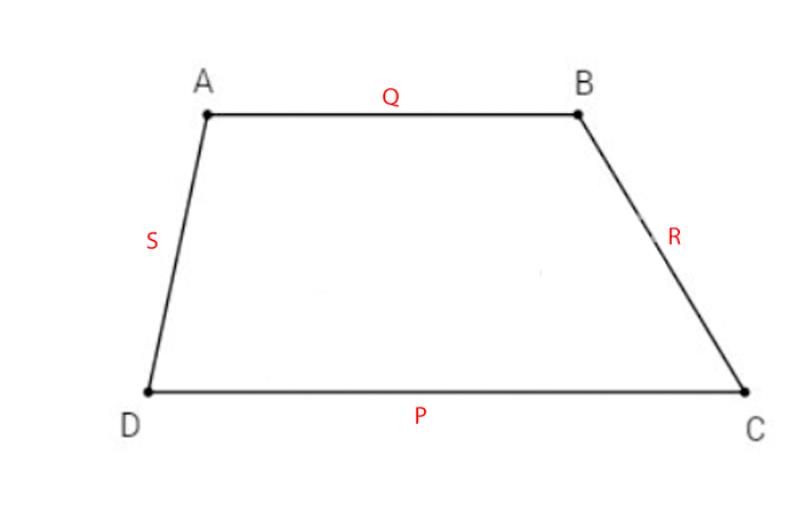
Cho hình thang ABCD có cạnh đáy AB, CD lần lượt là Q, P hai cạnh bên BC, AD lần lượt là R, S. Khi đó diện tích hình thang được xác định bằng:

\(\frac{(P+Q)\sqrt{2(R^2S^2+R^2(P-Q)^2+S^2(P-Q)^2)-(R^4+S^4+(P-Q)^4)}}{4(P-Q)}\)

Công thức tính diện tích của hình thang cũng có thể được xác định bằng một số phương pháp cắt dán hình thành các hình tam giác, hình chữ nhật. Tuy nhiên, ngoài công thức cơ bản thì công thức tính diện tích của hình thang khi biết bốn cạnh được sử dụng phổ biến nhất. Công thức này là hệ quả của Herong và một số công thức nâng cao khác.

6. Công thức tính chu vi hình thang

Hình thang là một đa giác có bốn cạnh có chu vi hình thang được xác định bằng độ dài của bốn cạnh cộng lại. Có thể hiểu rằng chu vi hình thang chính là phần độ dài giới hạn mặt phẳng diện tích.

Công thức tính chu vi của hình thang rất dễ dàng Bạn có thể hiểu qua ví dụ minh họa phía trên:

Cho hình thang ABCD, các cạnh lần lượt có độ dài a,b,c,d. Khi đó chu vi hình thang sẽ được xác định bằng

S= a+b+c+d

Công thức tính chu vi hình thang khá dễ nhớ so với công thức tính diện tích. Hầu như các em học sinh ít khi gặp khó khăn khi sử dụng công thức này.

7. Bài tập áp dụng tính chu vi, diện tích hình thang

Để củng cố lại phần kiến thức nói trên, các em hãy cũng Vieclam123.vn tham khảo một số bài tập cơ bản như sau:

Bài tập 1: Tính chu vi và diện tích hình thang ABCD biết độ dài đường cao kẻ từ A xuống cạnh CD bằng 25, hai cạnh đáy có độ dài lần lượt là 14,20 và hai cạnh bên có độ dài lần lượt là 5 và 7.

Lời giải: Diện tích hình thang ABCD = ½ (14+20)*25=425 (đơn vị diện tích)

Chu vi hình thang ABCD = 14+20+5+7=46 ( đơn vị độ dài)

Dạng bài toán như trên khá phổ biến tại bậc tiểu học. Chỉ cần nắm chắc công thức và tính toán cẩn thận có thể coi đây là một dạng bài không khó.

Chúng ta có thể thấy rằng hình thang là một trong những hình rất thông dụng trong cuộc sống cũng như trong các bài tập hình học. Các loại bài tập áp dụng công thức tính chu vi hình thang, diện tích hình thang vô cùng đa dạng, không chỉ ở hình học phẳng mà còn ở chương trình hình học không gian. Đối với các trường hợp đặc biệt, chúng ta cần áp dụng một cách linh hoạt để có thể ra được đáp số nhanh và chính xác nhất.

Bạn cần phải phân biệt được hình thang và các hình khác trước khi áp dụng công thức tính thức tính. Cần phải phân biệt được sự khác nhau giữa các hình như hình thang, hình bình hành, hình vuông, hình chữ nhật để tránh sự nhầm lẫn.

Có rất nhiều cách để có thể ghi nhớ công thức tính chu vi hình thang, diện tích hình thang. Trước hết bạn cần hiểu rõ bản chất công thức. Sau đó, có thể tham khảo một số bài thơ vui về công thức tính diện tích các hình. Học toán qua thơ sẽ giúp làm giảm đi sự khô khan của môn học này, giúp kiến thức ghim sâu vào bộ nhớ của bạn. Ở rất nhiều trường học, các thầy cô dạy toán thường sáng tác những bài thơ để học sinh có thể vừa vui vừa học tập một cách rất hiệu quả.

Để học tốt toán học nói chung và nắm chắc công thức tính chu vi hình thang, diện tích hình thang nói riêng, các bạn cần phải thường xuyên luyện tập và áp dụng các dạng bài tập khác nhau. Công thức tuy đơn giản nhưng tính ứng dụng rất cao đặc biệt là đối với các bài toán hóc búa của bậc trung học phổ thông. Vì vậy, hãy tạo cho mình một tiền đề kiến thức thật chắc chắn nếu như muốn thành công ở môn Toán học.

Trên bài viết này là toàn bộ những chia sẻ của mình về hình thang và công thức tính chu vi hình thang, diện tích hình thang. Hi vọng sẽ mang tới cho các bạn những thông tin hữu ích trong quá trình tìm hiểu.

>> Xem thêm: