Bảng Các Công Thức Lượng Giác Tổng Hợp và Cách Ghi Nhớ

Công thức lượng giác là kiến thức chúng ta được làm quen từ năm học lớp 8. Lên đến bậc trung học phổ thông, các bạn sẽ được tìm hiểu sâu rộng hơn về lượng giác và các dạng bài liên quan. Kiến thức về công thức lượng giác có tính ứng dụng rộng rãi không chỉ trên trường lớp mà còn ở bên ngoài thực tế. Ở bài viết dưới đây, các bạn hãy cùng Vieclam123.vn tìm hiểu đôi nét về các công thức tính lượng giác và những phương pháp học nhanh nhất.

MỤC LỤC

1. Những điều cần biết về Công thức lượng giác

Khái niệm: công thức lượng giác dùng để biểu thị một đại lượng tương quan giữa các cạnh và góc của một tam giác.

Trong các đề thi đại học, chuyên đề về lượng giác là một trong những chuyên đề không thể thiếu. Các bạn sẽ phải xử lý một số dạng bài như: phương trình lượng giác, khảo sát hàm số lượng giác và sử dụng lượng giác để giải quyết một số bài toán khác. Lượng giác còn có tính ứng dụng cao trong thiên văn học và trong lĩnh vực trắc địa. Các công thức tính lượng giác khá nhiều và có điểm “na ná” giống nhau. Vì vậy, các bạn cần phải hiểu bản chất của vấn đề và có mẹo học để tránh nhầm lẫn và có thể hoàn thành bài tập một cách tốt nhất.

$Sin A = \frac {a}{h}$ $Cos A = \frac {b}{h}$

$Tan A = \frac {Sin A}{CosA} = \frac{a}{b}$ $Cot A = \frac{CosA}{SinA} = \frac{b}{a}$

Bài thơ học công thức lượng giác cơ bản:

Sin: đi học (cạnh đối – cạnh huyền)

Cos: không hư (cạnh đối – cạnh huyền)

Tang: đoàn kết (cạnh đối – cạnh kề)

Cotang: kết đoàn (cạnh kề – cạnh đối)

Bài thơ ghi nhớ công thức tính tang, cotang:

Bắt được quả tang

Sin nằm trên cos

Côtang cãi lại

Cos nằm trên sin!

1.1. Yếu tố cần biết đề làm bài toán lượng giác

Hầu như chúng ta có thể giải được mọi câu hỏi về tam giác khi mà biết được một trong những yếu tố sau:

Độ lớn của hai cạnh và góc kề của chúng
Độ lớn của một cạnh và hai góc
Độ lớn của cả ba cạnh.

1.2. Nghiệm phương trình lượng giác cần nhớ

Kiến thức cơ bản

$\sin u = \sin v = \Leftrightarrow [\begin{matrix} u = v + 2k\pi \\ u = \pi -v + 2k\pi \end{matrix}$
$\cos u = \cos v = \Leftrightarrow [\begin{matrix} u = v + 2k\pi \\ u = -v + 2k\pi \end{matrix}$
$\tan u = \tan v \Leftrightarrow u = v + k\pi$
$\cot u = \cot v \Leftrightarrow u = v + k\pi$

Trường hợp đặc biệt

$\sin u = 0 \Leftrightarrow u = k\pi$
$\sin u = 1 \Leftrightarrow u = \frac{\pi}{2} + 2k\pi$
$\sin u = -1 \Leftrightarrow u = -\frac{\pi}{2} + 2k\pi$
$\cos u = 0 \Leftrightarrow u = \frac{\pi}{2} + k\pi$
$\cos u = 1 \Leftrightarrow u = 2k\pi$
$\cos u = -1 \Leftrightarrow u = \pi+2 k\pi$

1.3. Bảng giá trị lượng giác của một số cung đặc biệt

$\alpha$	0 $0^{\circ}$	$\frac{\pi}{6}$ $30^{\circ}$	$\frac{\pi}{4}$ $45^{\circ}$	$\frac{\pi}{3}$ $60^{\circ}$	$\frac{\pi}{2}$ $90^{\circ}$	$\frac{2\pi}{3}$ $120^{\circ}$	$\frac{3\pi}{4}$ $135^{\circ}$	$\frac{5\pi}{6}$ $150^{\circ}$	$\pi$ $180^{\circ}$
$\sin \alpha$	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
$\cos \alpha$	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0	$-\frac{1}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{\sqrt{3}}{2}$	-1
$\tan\alpha$	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	\|\|	$-\sqrt{3}$	-1	$-\frac{\sqrt{3}}{3}$	0
$\cot\alpha$	\|\|	$\sqrt{3}$	1	$\frac{\sqrt{3}}{3}$	0	$-\frac{\sqrt{3}}{3}$	-1	$-\sqrt{3}$	\|\|

2. Các công thức lượng giác cần nhớ

Các ký hiệu cơ bản của lượng giác gồm có : sin, cos, tan, cot. Những đại lượng này đều có mối liên hệ với nhau. Do các định lý đều đã được chứng minh, các bạn có thể ứng dụng luôn các công thức lượng giác để xử lý bài tập. Chỉ khi áp dụng đúng công thức, các bạn mới có thể tìm ra được nghiệm đúng của các phương trình lượng giác hoặc xử lý các bài toán hình phẳng, hình không gian theo đúng hướng.

Dưới đây là một số công thức lượng giác cơ bản để các bạn tham khảo.

2.1. Giá trị lượng giác các cung liên quan đặc biệt

2.2. Các hàm lượng giác cơ bản

2.3 Các hàm lượng giác nâng cao

2.4 Công thức nghiệm phương trình lượng giác

3. Phương pháp ghi nhớ công thức lượng giác

3.1. Học công thức lượng giác bằng thơ

Các công thức lượng giác rất dễ nhầm lẫn do khá giống nhau. Để có thể ghi nhớ dễ dàng, các bạn có thể sử dụng một số đoạn thơ vui. Có rất nhiều các bài thơ về công thức tính lượng giác được phổ biến rộng rãi với rất nhiều thế hệ học sinh. Cách học này giúp cho các bạn hạn chế nhầm lẫn và nhớ bài rất nhanh.Các bài thơ lượng giác thường là thơ vui và có vần điệu khá dễ thuộc, giúp cho môn Toán học đỡ khô khan, và giúp học sinh có hứng thú với học tập hơn.

Thực ra, học toán bằng thơ không phải là cách học mới. Đây có thể được coi là cách học công thức tính lượng giác dễ dàng nhất và được các thầy cô sử dụng nhiều nhất. Chẳng hạn khi các bạn học công thức nhân 3 bằng lời sẽ khó nhớ hơn rất nhiều so với việc học bằng thơ vui.

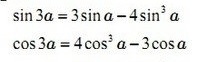
Nhân ba một góc bất kỳ

Sin thì ba, bốn, cos thì bốn ba

Dấu trừ đặt giữa hai ta

Lập phương chỗ bốn thế là ok

Hay với công thức cộng:

Sin thì sin cos cos sin

Cos thì cos cos sin sin dấu trừ.

Tang tổng thì lấy tổng tang

Chia một trừ với tích tang, dễ òm.

Khi đã phân tích và hiểu bản chất vấn đề, cách học bằng thơ sẽ giúp cho các bạn vừa học, vừa vui, vừa nhớ bài một cách nhanh chóng nhất. Hãy thử áp dụng những bài thơ “thần chú “ này trong quá trình học lượng giác của bạn nhé. Chương lượng giác sẽ trở nên dễ dàng hơn rất nhiều đấy!

Dưới đây là bài thơ “thần chú” về công thức tính lượng giác, các bạn có thể tham khảo và tìm hiểu thêm để sưu tập cho mình những công cụ để ghi nhớ kiến thức thật hiệu quả nhé!

Một số bài thơ để học công thức lượng giác nhanh hơn:

Sin bù, Cos đối,Tang Pi,

Phụ nhau Sin Cos, ắt thì phân chia

Giải thích: Cosin của hai góc đối bằng nhau; sin của hai góc bù nhau thì bằng nhau; phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia; tan của hai góc hơn kém pi thì bằng nhau.

Công thức cộng

Cos cộng cos bằng hai cos cos

cos trừ cos bằng trừ hai sin sin

Sin cộng sin bằng hai sin cos

sin trừ sin bằng hai cos sin.

Sin thì sin cos cos sin

Cos thì cos cos sin sin “coi chừng” (dấu trừ).

Tang tổng thì lấy tổng tang

Chia một trừ với tích tang, dễ òm.

Công thức nhân 3:

Nhân ba một góc bất kỳ,

sin thì ba bốn, cos thì bốn ba,

dấu trừ đặt giữa hai ta, lập phương chỗ bốn,

... thế là ok.

Công thức gấp đôi:

+Sin gấp đôi = 2 sin cos

+Cos gấp đôi = bình cos trừ bình sin = trừ 1 cộng hai lần bình cos = cộng 1 trừ hai lần bình sin.

+Tang gấp đôi

Tang đôi ta lấy đôi tang (2 tang), Chia 1 trừ lại bình tang, ra liền.

Cách nhớ công thức: tan(a+b)=(tan+tanb)/1-tana.tanb là

tan một tổng hai tầng cao rộng
trên thượng tầng tan cộng tan tan
dưới hạ tầng số 1 ngang tàng
dám trừ một tích tan tan oai hùng

Công thức biến tích thành tổng:

Cos cos nửa cos-cộng, cộng cos-trừ
Sin sin nửa cos-trừ trừ cos-cộng
Sin cos nửa sin-cộng cộng sin-trừ

Công thức biến tổng thành tích:

sin tổng lập tổng sin cô
cô tổng lập hiệu đôi cô đôi chàng
còn tan tử cộng đôi tan (hoặc là: tan tổng lập tổng hai tan)
một trừ tan tích mẫu mang thương sầu
gặp hiệu ta chớ lo âu,
đổi trừ thành cộng ghi sâu vào lòng

3.2. Thường xuyên làm bài tập các công thức lượng giác

Môn Toán học đòi hỏi người học phải đào sâu suy nghĩ và hiểu bản chất của vấn đề. Các bạn sẽ gặp rất nhiều khó khăn nếu như không biết cách áp dụng công thức. Hơn nữa, các dạng bài lượng giác rất đa dạng. Nếu không luyện tập thường xuyên việc ghi nhớ bạn sẽ rất khó để chinh phục được chuyên đề này.

Đầu tiên, các bạn hãy hoàn thành tất cả các dạng bài trong sách giáo khoa và trong sách bài tập. Khi đã thực sự nắm chắc các công thức lượng giác qua việc luyện những dạng bài cơ bản này, hãy tìm tới sách nâng cao của một số tác giả nổi tiếng như nhóm Cự Môn,… để có thể ôn luyện một cách bài bản nhất. Trong quá trình luyện tập này, các công thức tính lượng giác sẽ được “ ghim” tự động được ghim vào bộ nhớ của bạn.

Không chỉ riêng đối với các công thức tính lượng giác, mà trong tất cả mọi chuyên đề Toán học khác, việc luyện tập thường xuyên sẽ giúp bạn nhìn ra được rất nhiều những điểm thú vị và có kỹ năng áp dụng kiến thức thuần thục. Khi đã rèn luyện được tư duy, mọi vấn đề đều trở nên dễ dàng hơn rất nhiều.

Học Toán nói chung và học công thức lượng giác nói riêng phải cần một quá trình dài. Lượng giác có thể được coi là kiến thức mắt xích không chỉ ứng dụng trong hình học mà còn có rất nhiều các ứng dụng đại số thú vị khác như : đồ thị lượng giác, số phức bằng lượng giác, tích phân, nguyên hàm lượng giác. Các bạn cần phải thật chắc chắn kiến thức thì mới có thể xử lý được tất cả các dạng bài một cách nhanh chóng nhất!

Các bạn học sinh vẫn thường truyền tai nhau :” Khó như lý, bí như hình, linh tinh như đại “.. Trong quá trình học Toán, phương pháp học vô cùng quan trọng và quyết định phần lớn thành công của các bạn. Vì thế, ngay từ khi làm quen với những kiến thức phổ thông cơ bản là công thức lượng giác, hãy tạo cho mình một nền tảng thật vững chắc để dễ dàng hơn trong việc chinh phục môn Toán.

>> Xem thêm: