1. Tìm hiểu tích phân là gì?

1.1. Khái niệm

Tích phân là một phép toán cơ bản của toán học giải tích, ngược với tích phân là vi phân. Chúng ta có thể hiểu tích phân chính là diện tích hay diện tích tổng quát. Trong hình học có rất nhiều hình cần chúng ta phải chia nhỏ ra thì mới có thể tính diện tích được. Nhưng sẽ có một số hình chứa những hình thang cong, và tích phân chính là công cụ giúp chúng ta tính diện tích hình thang cong đó.

Giải thích theo hình học thì ta có: Tích phân của một hàm f(x) từ điểm a tới điểm b chính là diện tích của vùng trong không gian phẳng x0y được tạo bởi đồ thị f(x) với trục hoành 0x. Trong đó tích phân sẽ bằng tổng điện tích phía trên trục hoành trừ cho diện tích vùng dưới.

Một số công thức tính tích phân cần nhớ:

1.2. Tính chất của tích phân

Khi học về các công thức tích phân, bạn không chỉ cần nắm chắc khái niệm mà còn cần nắm chắc và áp dụng tốt tính chất của tích phân vào bài tập nữa. Sau đây là những tính chất của tích phân:

2. Các công thức tích phân thường xuyên có trong thi đại học 

Nội dung tích phân ở cấp 3 được áp dụng nhiều trong đề thi đại học. Đây là phần kiến thức quan trọng trong học phổ thông cuối cấp mà các bạn học sinh cần học chắc kiến thức cũng như áp dụng thành thạo vào làm các dạng bài tập tương ứng. Sau đây là các công thức tích phân thường có trong đề thi đại học các năm hãy tham khảo nhé.                    

2.1. Hàm phân thức        

2.2. Lôgarit        

2.3. Hàm mũ      

2.4. Hàm vô tỉ    

2.5. Hàm lượng giác       

2.6. Hàm hypebolic         

3. Bài tập áp dụng công thức tích phân 

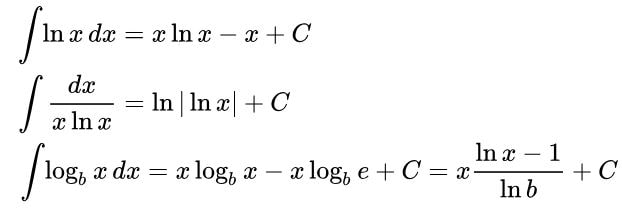
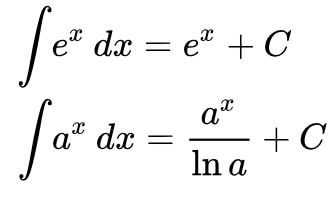
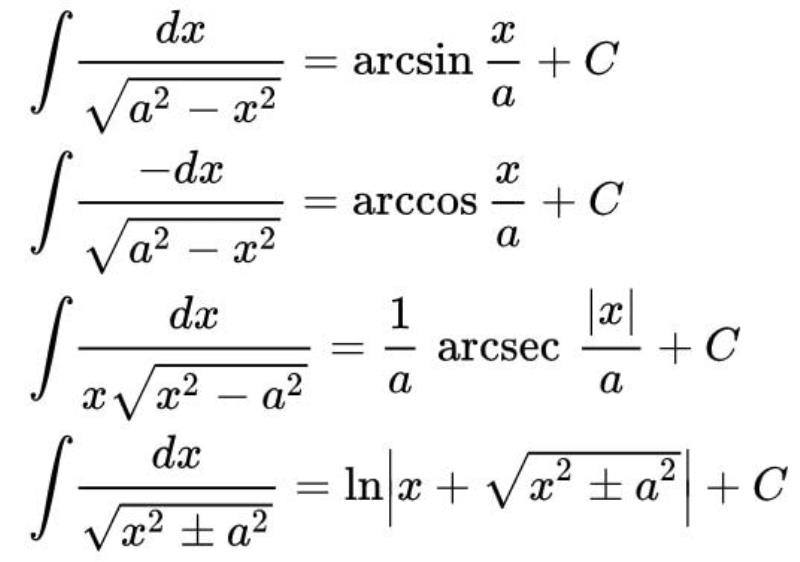
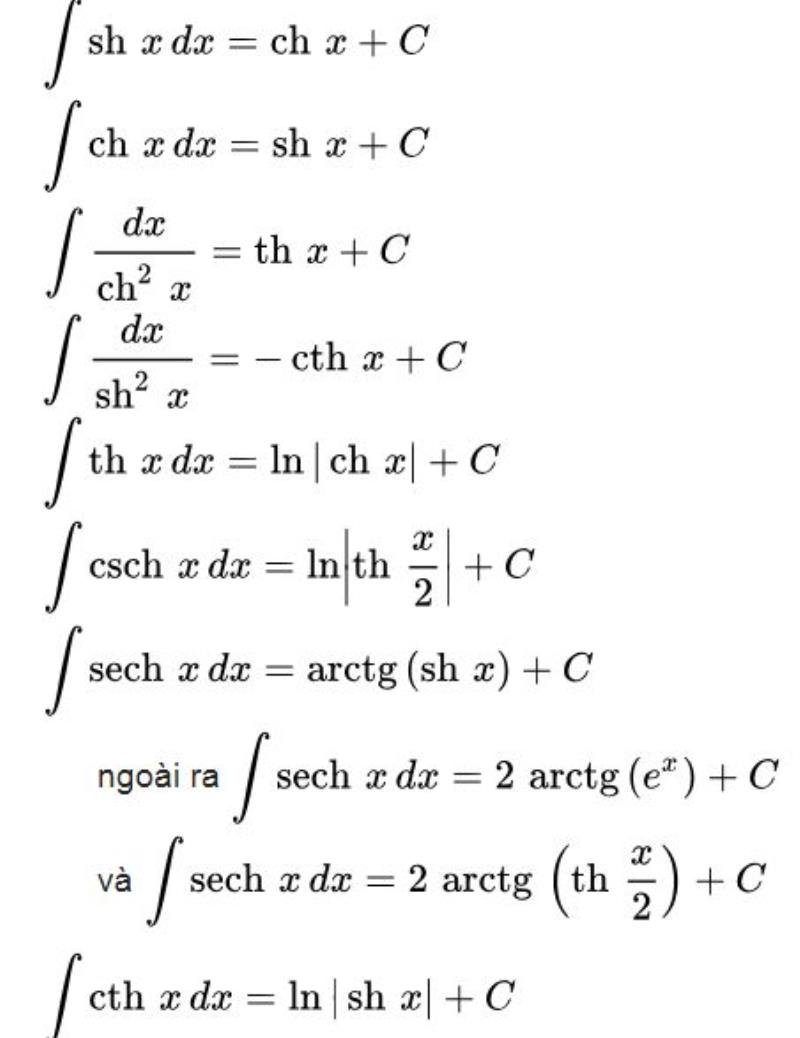
Để bạn ghi nhớ kiến thức cùng công thức của tích phân, chúng ta cùng làm thử các ví dụ sau đây nhé.

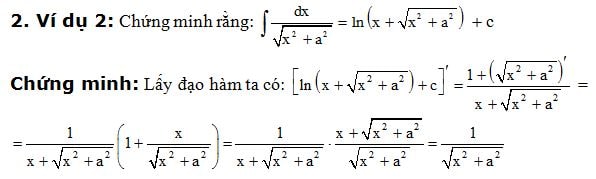
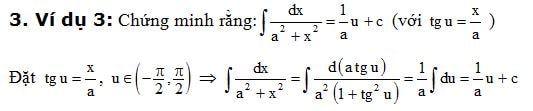
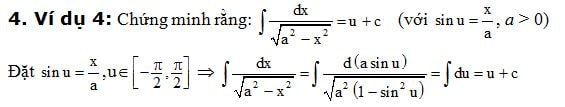
Trên đây có rất nhiều kiến thức cùng công thức tích phân quan trọng mà bạn cần nhớ. Hy vọng những nội dung về công thức tích phân và bảng tích phân chi tiết ở trên đã mang tới cho bạn những kiến thức bổ ích. 

>> Xem thêm:

• Công thức tính chu vi, diện tích tam giác
• Đạo hàm và công thức đạo hàm cần biết
• Định lý Vi-et và những điều cần biết