Định lý Viet là kiến thức quan trọng trong chương trình học chính khóa đối với học sinh. Sau đây là những thông tin về định lý Vi-et và những điều cần biết.
MỤC LỤC
Định lý Viet là công thức thể hiện mối quan hệ giữa các nghiệm của phương trình đa thức trong trường số phức và các hệ số do nhà toán học Pháp François Viète tìm ra. Viète được phiên âm theo tiếng Việt là Vi-ét.
Định lý Vi-et học ở chương trình đại số ở cấp 2 và cấp 3 có nội dung kiến thức quan trọng đối với học sinh.


Theo hệ thức Vi-et, phương trình \(ax^2 + bx + c = 0\) (2) với a≠0 có hai nghiệm là x1, x2 khi và chỉ khi thỏa mãi các hệ thức:
\(x_1 + x_2 = \frac{-b}{a}\)
và
\(x_1*x_2 = \frac{c}{a}\)
Từ hệ thức viet chúng ta có thể áp dụng để tìm 2 số a và b khi biết a+b=S và a.b=P, khi đó ta chỉ cần giải phương trình \(x^2-Sx+P=0\), a và b chính là 2 nghiệm của phương trình.
Do đó, các ứng dụng của Định lý Vi-et bao gồm:
• Tính nhẩm nghiệm phương trình bậc 2. Ví dụ: Với phương trình \(x^2 – 5x + 6 = 0\), ta có thể tính nhẩm nghiệm số nguyên của phương trình là 2 và 3 bởi 2 + 3 = 5 và 2 x 3 = 6.
• Tìm 2 số khi biết tích và tổng: Nếu tổng là S, tích là P thì hai số có 2 nghiệm phương trình gồm : \(x^2 – Sx + P = 0\) (Lưu ý, hai số trên tồn tại với điều kiện là \(S^2 – 4P >= 0\))
• Tính giá trị các biểu thức đối xứng của 2 nghiệm phương trình bậc 2:
• Biến tam thức bậc 2 thành nhân tử: Nếu x1, x2 là nghiệm của đa thức \(f(x) = ax^2 + bx + c\) có thể phân tích thành nhân tử f(x) = a(x – x1)(x – x2)
Xem thêm: Bảng công thức đạo hàm tổng hợp kèm bài tập ví dụ
Công thức Vi-ét thể hiện theo phương trình bậc 2 có dạng như sau nếu 2 nghiệm của phương trình lần lượt là x1 và x2, ta có công thức:
\(ax^2 + bx + c = 0\), điều kiện a # 0 thì ta có x1 + x2 = S = -b/a và x1.x2 = P = c/a
Xem thêm: Toàn bộ chi tiết về công thức LOGARIT cần biết
Phương trình \(ax^3 + bx^2 + cx + d = 0\) có 3 nghiệm phân biệt x1, x2, x3 khi đó:
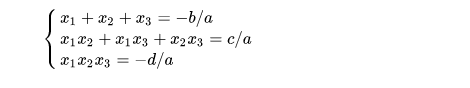
Lưu ý: Áp dụng Định lý viet bậc 3 giúp giải một số bài phương trình bậc 3 dễ dạng hơn
Phương trình đa thức bất kỳ có dạng: 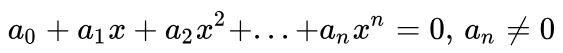
Cho x1, x2, x3,…, xn là n nghiệm của phương trình đa thức ở trên, ta có công thức như sau: 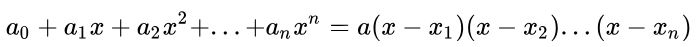
Do đó, công thức Vi-ét sẽ là kết quả của phép tính ở vế phải và ta được:
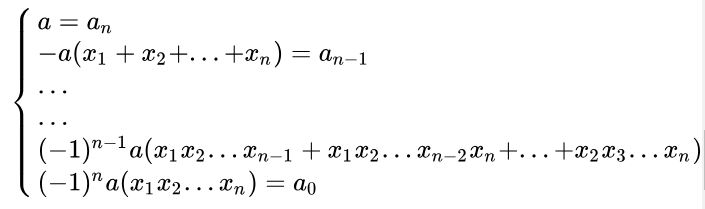
Theo đó, trong hàng k bất kỳ, ta sẽ có đẳng thức \(a_{n-k}\) sẽ là vế phải còn vế trái sẽ là:

Ví dụ về phương trình bậc 3 cho x1, x2, x3 là nghiệm của phương trình: \(ax^3 + bx^2 + cx + d = 0\)
Ta chia đều cho a3 tức a ở cả 2 về của phương trình đồng thời chuyển dấu trừ (nếu có) sang về phải thì công thức Vi-et là:
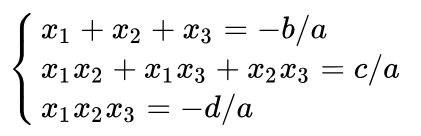

.JPG)


.JPG)
.JPG)




.JPG)


.JPG)

.JPG)





.JPG)
.JPG)

.JPG)


Dựa trên cơ sở của định lý Vi-et, ta thiết lập phương trình bậc 2 có nghiệm là x1, x2. Nếu x1+x2=S; x1.x2=P thì nghiệm của phương trình là x1, x2
Xét các ví dụ:
.JPG)








Sau đây là những bài tập áp dụng định lý Vi-et đã học ở trên mà chúng ta cùng tham khảo sau đây.
Bài tập 1: Gọi các nghiệm của phương trình \(x^2 – 3x + 1 = 0\) là x1, x2. Yêu cầu tìm giá trị của các biểu thức mà không giải phương trình.

Bài giải: Có Δ = -3^2 – 4.1 = 9 – 4 = 5 > 0 => phương trình có nghiệm x1, x2 # 0
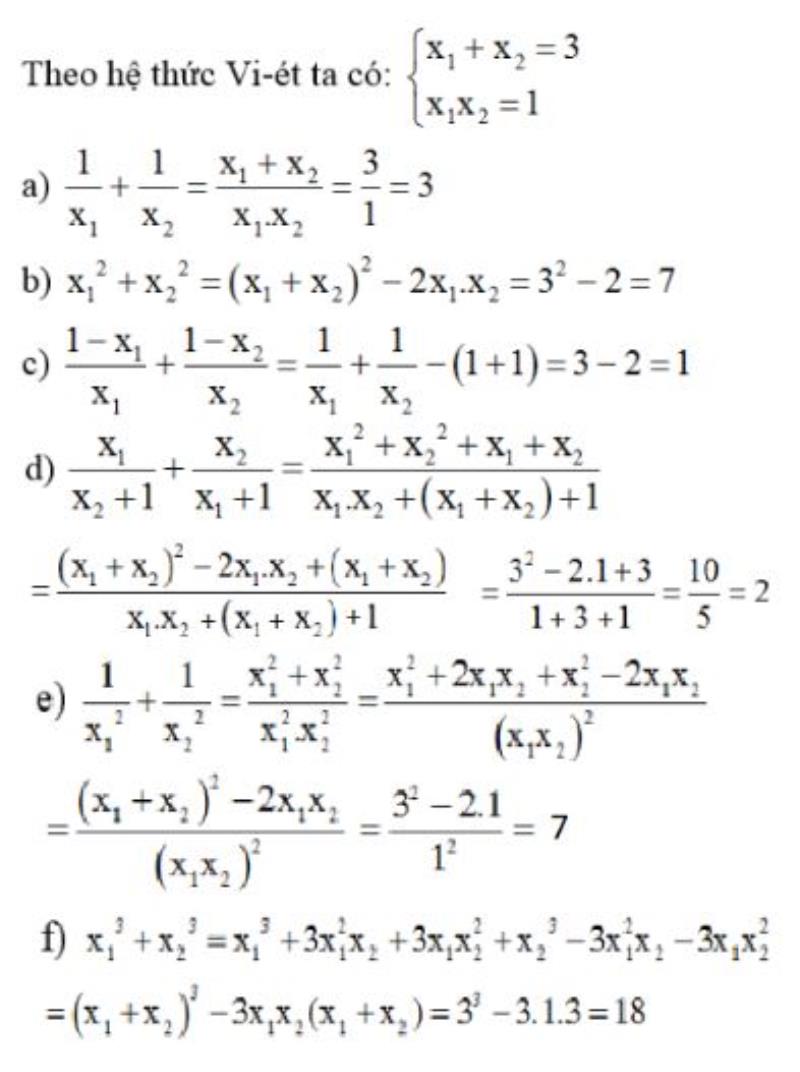
Bài tập 2: Đề bài có phương trình x^2 + (2m – 1)x – m = 0
a. Chứng minh với mọi m phương trình luôn có nghiệm.
b. Gọi x1, x2 là 2 nghiệm. Để biểu thức A=\(x_1^2 + x_2^2 - x_1.x_2\) có giá trị nhỏ nhất hãy tìm giá trị của m.
Bài giải:
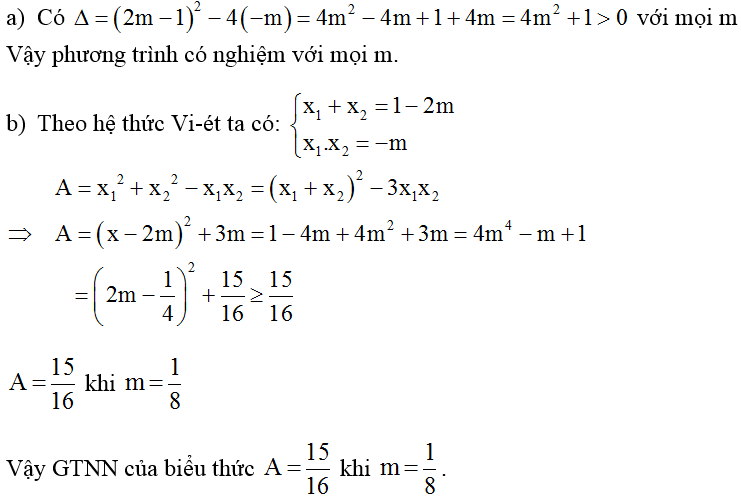
Bài tập 3: Tìm giá trị của k của phương trình x^2 + 2x + k = 0 để nghiệm x1, x2 thỏa mãn 1 trong các điều kiện như sau:
Bài giải:
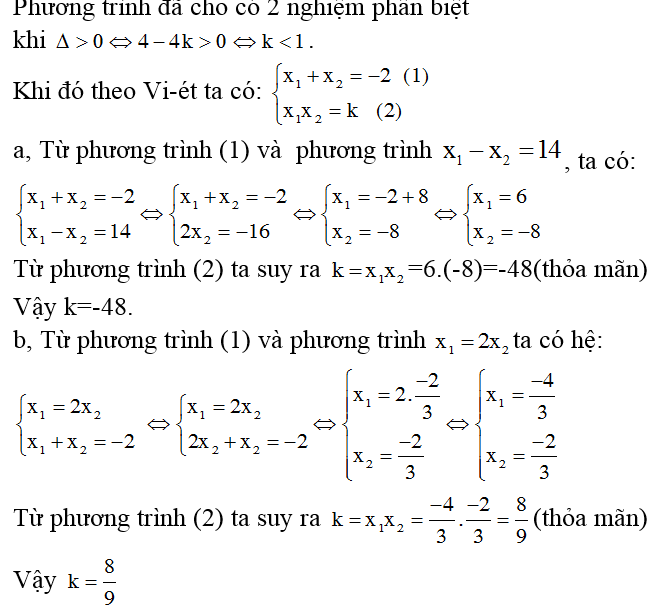
Hy vọng những kiến thức về định lý Vi-ét ở trên đã mang tới cho bạn những thông tin mà mình đang cần. Cùng học tốt môn toán mỗi ngày bằng cách truy cập và làm bài tren vieclam123.vn nhé.
>> Xem thêm:
MỤC LỤC




Chia sẻ