Bất phương trình là một dạng toán thường gặp trong các đề thi và cũng thường xuyên xuất hiện trong các đề thi quan trọng như đề thi THPT Quốc gia. Ở bài viết dưới đây, Vieclam123.vn xin gửi tới các bạn một số kiến thức liên quan đến bất phương trình và một số phương pháp giải bất phương trình cơ bản.
MỤC LỤC
Khác với phương trình, bất phương trình có hai vế không bằng nhau, có thể lớn hơn hoặc nhỏ hơn. Nghiệm của bất phương trình không phải chỉ là một giá trị mà sẽ bao gồm cả một tập hợp giá trị thỏa mãn điều kiện của bất phương trình.
\(f(x)>g(x), f(x)
Có rất nhiều dạng bất phương trình khác nhau như : bất phương trình bậc một, bất phương trình bậc hai, bất phương trình vô tỷ, bất phương trình chứa căn, bất phương trình logarit. Mỗi dạng bài lại có một cách giải bất phương trình khác nhau, tùy theo đặc điểm của bất phương trình.
Có hai quy tắc cơ bản trong giải bất phương trình là quy tắc chuyển vế và quy tắc nhân.
Nhắc đến quy tắc chuyển vế trong giải bất phương trình bạn có thể nhớ nhanh bằng cụm từ chuyển vế, đổi dấu. Khi chuyển một hạng tử của bất phương trình sang vế khác, bạn cần phải chú ý đổi dấu của hàng tử đó
Quy tắc nhân với một số cũng tương đối đơn giản. Khi nhân cả hai vế của bất phương trình với một số dương, bạn giữ nguyên chiều và ngược lại khi nhân cả hai vế với số âm bạn cần đổi chiều của bất phương trình.
Bất phương trình cơ bản có dạng khá đơn giản, thường là bất phương trình bậc nhất, không xuất hiện lũy thừa và căn thức. Đối với giải bất phương trình này, bạn có thể xác định tập nghiệm rất dễ dàng bằng việc áp dụng hai công thức cơ bản của bất phương trình. Thông thường, những bất phương trình vô tỷ đều phải đưa về dạng này để có thể tìm được nghiệm đúng.
Cho hàm số \(f(x) = a.x+b >0\) (a khác 0)
Ta có thể dễ dàng tính được nghiệm của phương trình \(x > {b \over a}\)
Bất phương trình bậc hai là một dạng phổ biến trong các đề thi đại trà. Đối với bất phương trình này, bạn cần phải đưa bất phương trình dạng f(x)>g(x) về dạng: \(ax^2+bx+c > 0\)
Khi đó, bạn phân tích tam thức bậc hai thành nhân tử và tìm khoảng nghiệm của bất phương trình trên bảng xét dấu. Bạn có thể nhớ quy tắc “ trong trái- ngoài cùng” để áp dụng khi tìm khoảng nghiệm của bất phương trình này.
Với bất phương trình: \(ax^2+bx+c > 0\) (a khác 0)
Ta tính: \( Δ = b^2 - 4.a.c\)
Trường hợp 1: Nếu Δ > 0 thì phương trình có 2 nghiệm x1 và x2 (x1
Khi đó ta có:
Trường hợp 2: Nếu Δ = 0
Trường hợp 3: Nếu Δ < 0
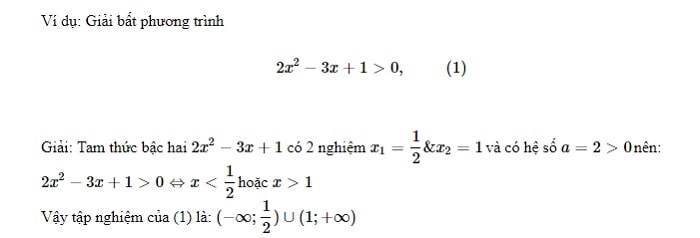
Đây là một trong những dạng khó nhất của bất phương trình. Những phương trình này thường không được giải theo một quy tắc nào cả.
Bạn có thể áp dụng một số ứng dụng của chương khảo sát hàm số vào để giải bất phương trình dạng này. Ngoài ra có thể nhân liên hợp và đặt ẩn phụ để có thể tìm ra được khoảng nghiệm chính xác.
Trường hợp gặp bất phương trình vô tỷ,bạn cần phân tích kỹ đặc điểm của bài tập để tìm ra được hướng giải bất phương trình. Khi luyện tập nhiều, bạn sẽ phản xạ nhanh hơn với dạng bài này. Đây là một trong những câu phân loại học sinh của đề thi đại học, đòi hỏi tư duy cao ở học sinh.
Khi giải bất phương trình chứa căn, các bạn cần phải lưu ý một số về điều kiện xác định của căn thức . Đây là một trong những lưu ý quan trọng khi bạn thực hiện giải bất phương trình chứa căn.
Cách giải phổ biến nhất của bất phương trình dạng này thường là nhân với liên hợp để đưa về dạng phương trình bậc hai hoặc phương trình cơ bản. Ngoài ra, một số trường hợp bất phương trình chứa căn còn đồng thời là phương trình vô tỷ. Bạn cần phải thử các cách khác nhau mới có thể tìm ra được cách giải đúng
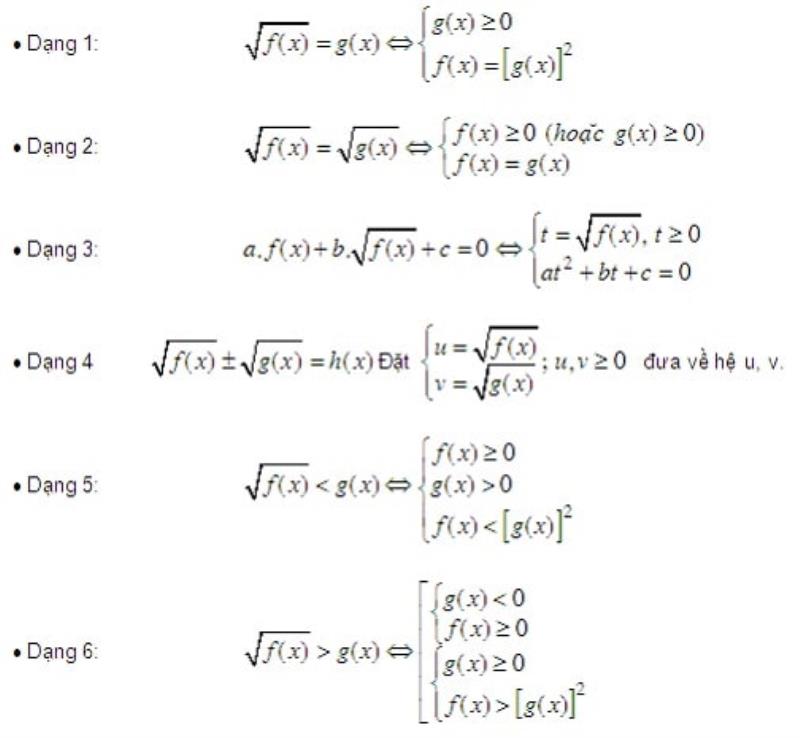
Bất phương trình chứa mũ cao thường có thể áp dụng phương pháp khảo sát hàm số và phân tích đa thức thành nhân tử. Đây là một dạng phương trình khó và yêu cầu các bạn phải có sự quan sát, phân tích cẩn thận.
Muốn giải tốt bất phương trình logarit, các bạn cần phải thành thạo các quy tắc của về logarit, mũ để có thể áp dụng vào tìm tập nghiệm của bất phương trình. Dạng bất phương trình này thường được đưa về phương trình mũ để tìm ra tập nghiệm
Khi bất phương trình có dấu giá trị tuyệt đối, bạn cần phải nắm rõ các quy tắc về dấu giá trị tuyệt đối để có thể bỏ dấu giá trị tuyệt đối và tìm ra nghiệm đúng của bất phương trình. Dạng bài này thường không quá khó, xuất hiện chủ yếu ở các đề thi và đề kiểm tra đại trà
Đây là một dạng bài tập khó, và xuất hiện khá nhiều trong những câu phân loại học sinh của các đề thi trung học phổ thông quốc gia. Các bạn cần nắm chắc kiến thức về chương khảo sát hàm số để có thể làm tốt dạng bài này.
Trên đây là những chia sẻ sơ lược về bất phương trình. Các bạn có thể đọc thêm một số cuốn sách tham khảo để nâng cao vốn kiến thức. Chúc các bạn thành công khi chinh phục phần hành kiến thức bất phương trình nói riêng và môn Toán học nói chung.
>> Xem thêm:
MỤC LỤC




Chia sẻ