Công thức tính chu vi, diện tích tam giác là một trong những công thức chúng ta được làm quen từ bậc tiểu học. Chúng ta cần ghi nhớ thật kỹ công thức này vì sẽ cần áp dụng nó rất nhiều sau này.
MỤC LỤC
Trước tiên, chúng ta cần phải nắm được diện tích là gì? Diện tích thực chất là phần mặt phẳng giới hạn bởi các cạnh của đa giác. Đối với mỗi hình, lại có một công thức tính riêng. Trong đó, diện tích của tam giác là một trong những công thức phổ biến, thường xuyên được sử dụng trong các bài toán từ thời tiểu học. Dưới đây, là công thức tính của tam giác thường và một số tam giác dạng đặc biệt.
Đây có thể được coi là công thức gốc cho tất cả các công thức mở rộng. Ví dụ ta có tam giác có một cạnh là a, chiều cao tương ứng so với cạnh này được từ đỉnh còn lại được ký hiệu là h. Khi đó, công thức tính diện tích được xác định như sau :
\(S = {ah \over2}\)
Đây là một trong những công thức thông dụng nhất.
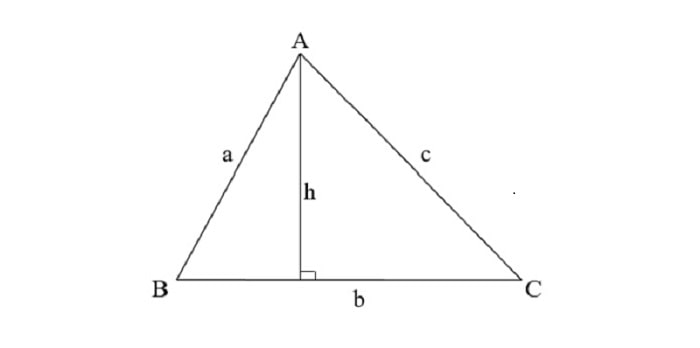
Diện tích tam giác được xác định bằng một phần hai của cạnh đáy nhân với chiều cao tương ứng
Ngoài ra, ở các chương trình học cao hơn, các bạn có thể sử dụng hệ thức hê rông để tính diện tích của tam giác, khi biết độ dài ba cạnh.
Ví dụ , a, b,c lần lượt là độ dài 3 cạnh của 1 tam giác.
Khi đó ta có nửa chu vi tam giác là
\(P = {a+b+c \over 2}\)
Áp dụng hệ thức Hê- rông, diện tích tam giác sẽ được tính như sau
\(S=\sqrt{P(P-a)(P-b)(P-c)}\)
Hệ thức Hê-rông được áp dụng bắt đầu từ bậc phổ thông, và có tính ứng dụng khá cao để giải các bài toán hình học phức tạp.
Ngoài hai công thức trên, bạn cũng có thể áp dụng công thức tính diện tích của tam giác bằng sin như sau:
Ba cạnh của một tam giác lần lượt là a,b,c, các góc được tạo bởi các cạnh lần lượt là A,B,C. Khi đó ta có thể tính diện tích của tam giác như sau:
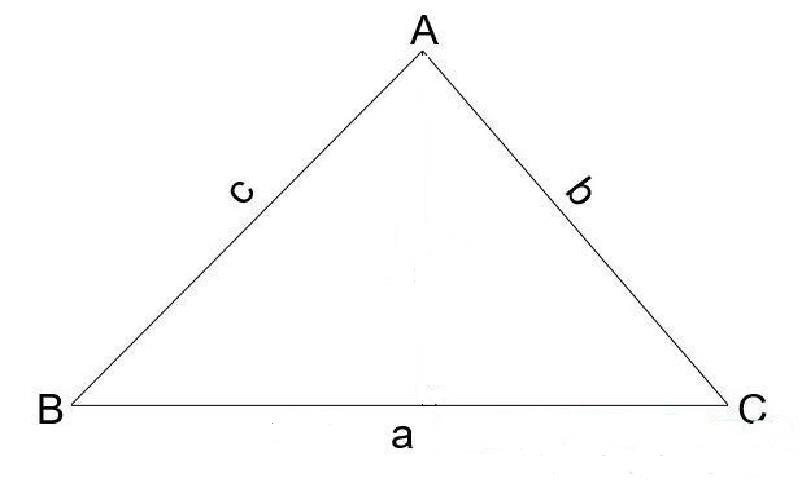
\(S= {a.b.sinC \over 2} = {a.c.sin B \over 2}= {b.c.sin A \over 2} \)
Công thức tính diện tích của tam giác đều cũng dựa trên nguyên lý của công thức tính diện tích của tam giác tam giác thường. Tuy nhiên do đây là trường hợp đặc biệt có chiều cao trùng với đường trung tuyến, nên ta có thể áp dụng công thức tính nhanh khi biết cạnh của tam giác.
Ví dụ, có tam giác đều, cạnh bằng a
Khi đó ta có công thức tính diện tích tam giác như sau:
\(S=a\sqrt3/4\)
Tam giác vuông là một trong những trường hợp đặc biệt, có hai cạnh tạo với nhau một góc 90 độ, gọi là hai cạnh góc vuông
Ví dụ, có tam giác vuông có hai cạnh góc vuông lần lượt là a và b
Khi đó, công thức tính diện tích của tam giác sẽ là
S= ab/2
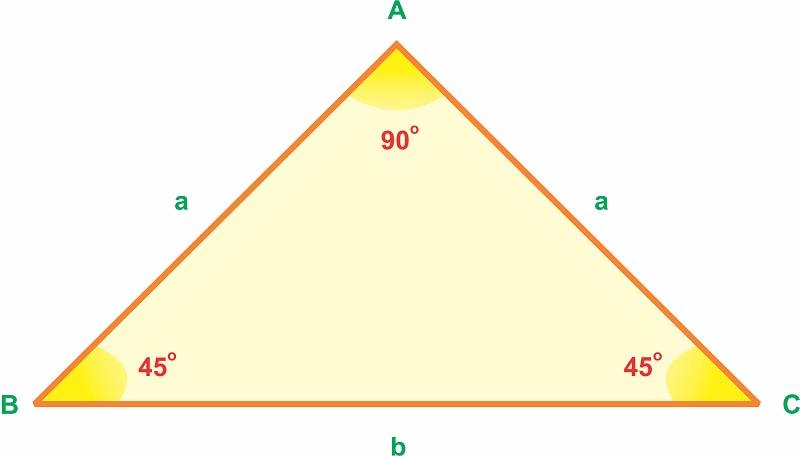
Ngoài công thức cơ bản một số trường hợp đặc biệt được áp dụng công thức riêng
Đối với một tam giác, có thể hiểu rằng chu vi tam giác chính là tổng độ dài của các cạnh tạo nên tam giác đó
Ví dụ khi có a,b,c lần lượt là độ dài 3 cạnh của một tam giác, ta sẽ có chu vi tam giác là
P= a+b+c
Để ghi nhớ một công thức, cách đơn giản nhất là thường xuyên tiếp xúc với nó. Bạn thường xuyên làm các bài tập và áp dụng thường xuyên, việc ghi nhớ công thức sẽ trở nên vô cùng đơn giản và nhanh chóng. Đối với những bạn có niềm đam mê toán học, chỉ sau một vài bài tập thực hành là có thể dễ dàng thuộc nằm lòng công thức tính diện tích, chu vi tam giác . Nếu trí nhớ của bạn không tốt, trong quá trình học, có thể ghi công thức ra nháp hoặc sổ tay. Một thời gian dài sử dụng, sẽ khiến cho nó được nạp vào bộ nhớ của bạn một cách tự nhiên nhất.
Việc sử dụng thơ vui trong quá trình ghi nhớ các công thức đã trở nên rất phổ biến.Rất nhiều thầy cô, gia sư đã sáng tác ra những vần thơ khá dễ thuộc, có vần điệu để học sinh dễ nhớ công thức tính diện tích, chu vi các hình hơn. Tôi còn nhờ một câu thơ về diện tích tam giác của cô giáo thời tiểu học:
Diện tích tam giác khó chi
Chiều cao nhân đáy ta thời chia đôi
Tất nhiên, sau này, khi chương trình học nâng cao hơn, bạn còn cần phải nhớ những cách khác để có thể tính diện tích của tam giác, chu vi tam giác trong các trường hợp khác nhau. Tuy nhiên nếu gặp khó khăn trong việc ghi nhớ các công thức nâng cao, bạn có thể dùng công thức cơ bản và áp dụng các tính chất của tam giác để có thể tìm ra phương hướng xử lý trong bài toán.
Từ xưa, học toán bằng thơ luôn được các thầy cô lựa chọn làm phương pháp để làm giảm đi sự căng thẳng và khô khan của các con số. Vì thế, nếu có thời gian, bạn hãy sưu tầm cách tính diện tích tam giác, chu vi tam giác bằng thơ trên mạng internet để vừa học, vừa vui nhé!
Công thức tính diện tích, chu vi tam giác có thể được áp dụng trong một số câu hỏi trắc nghiệm Toán học đơn giản, cũng có thể được dùng để áp dụng trong những dạng toán phức tạp hơn như quỹ tích, dựng hình. Trong chương trình phổ thông, các công thức này cũng là công cụ hỗ trợ đắc lực cho việc xử lý các bài toán hình học không gian hóc búa.
Ví dụ 1: Tính chu vi hình tam giác có các cạnh lần lượt là 5cm, 3cm, 1dm
Giải: Trước khi tính chu vi hình tam giác ta cần đồng nhất đơn vị đo. 1dm=10cm
Ta có P=5+3+10=18cm
vậy chu vi hình tam giác bằng 18cm.
Ví dụ 2: Tính diện tích hình tam giác khi biết cạnh đáy bằng 12cm và chiều cao bằng 8cm.
Giải: Áp dụng công thức tính diện tích hình tam giác ta được: S = (12.8)/2=48cm2
Ví dụ 3: Tính diện tích hình tam giác khi biết độ dài 3 cạnh lần lượt là 3cm, 7cm, 8cm.
Giải: Áp dụng công thức tính diện tích hình tam giác bằng chu vi: \(S=\sqrt{P(P-a)(P-b)(P-c)}\)
Ta có nửa chu vi hình tam giác là: (3+7+8)/2=9
Khi đó diện tích \(S=\sqrt{P(P-a)(P-b)(P-c)} = \sqrt{9(9-3)(9-7)(9-8)} = 10.39cm^2\)
Ngoài ra còn rất nhiều dạng bài tập tính chu vi diện tích hình tam giác khác. Các bạn hãy dựa vào dữ liệu đề bài và những công thức mà vieclam123.vn cung cấp để hoàn thành tốt bài tập của mình nhé.
Trên đây là những chia sẻ đơn giản về công thức tính diện tích, chu vi tam giác. Rất mong có thể cung cấp những thông tin hữu ích cho những bạn đang có thắc mắc về những công thức này.
>> Xem thêm bài viết liên quan:
MỤC LỤC




Chia sẻ