MỤC LỤC
Đường tròn là tập hợp tất cả các điểm nằm trên một mặt phẳng cách đều một điểm cho trước cố định một khoảng. Khoảng này được gọi là bán kính. Điểm cho trước cố định được gọi là tâm của đường tròn. Ngoài ra khi nhắc về đường tròn, đường kính cũng là một khái niệm cần nắm được. Nó chính là độ dài của đoạn thẳng giới hạn bởi ba điểm thẳng hàng bao gồm hai điểm bất kỳ nằm trên đường tròn và tâm của đường tròn. Như vậy có thể hiểu rằng, đường kính có chiều dài gấp đôi bán kính.
Hình tròn chính là phần mặt phẳng được giới hạn bởi đường tròn. Các khái niệm này, có phần phức tạp hơn đôi chút so với các hình đa giác, có thể dễ dàng đo được độ dài của từng cạnh bằng thước đo độ dài.

Hình ảnh hình tròn và các kiến thức cơ bản cần biết
Trước khi đi vào công thức tính diện tích hình tròn, công thức tính chu vi hình tròn, tôi xin khái quát sơ lược về khái niệm chu vi và diện tích. Hai khái niệm này rất dễ nhầm lẫn, đặc biệt là đối với hình tròn, vì đây là một trong những hình khá đặc biệt so với những hình mà các bạn được học trong hình học phẳng.
Chu vi có thể hiểu nó là một đường bao quanh diện tích và chính là độ dài của đường bao quanh này. Còn diện tích là độ đo dùng để đo độ lớn của bề mặt được giới hạn bởi một hình.
Hình tròn là một trong những hình đặc biệt, không được giới hạn bởi các đường thẳng như các đa giác, chính vì thế, công thức tính diện tích diện tích hình tròn, công thức tính chu vi hình tròn còn được thể hiện qua một hằng số cố định là số Pi, được ký hiệu là π. Hằng số Pi có giá trị xấp xỉ bằng 3.14, đã được các nhà toán học Hy Lạp tìm ra và chứng minh. Đây là một hằng số bắt buộc các bạn cần phải nhớ trong quá trình học các kiến thức về hình tròn, đặc biệt là công thức tính chu vi, diện tích
Sau khi đã đưa ra những khái quát sơ lược về các kiến thức đơn giản liên quan đến hình tròn, tôi xin gửi tới các bạn hai công thức tính diện tích hình tròn, công thức tính chu vi hình tròn để tham khảo:
Chu vi hình tròn là độ dài đường bao quanh hay đường biên giới hạn của đường tròn (chu vi hình tròn bằng độ dài đường tròn). Công thức tính chu vi hình tròng bằng đường kính (2 lần bán kính) nhân với số Pi (3.14).
Trong quá trình nghiên cứu, các nhà toán học đã chỉ ra rằng: chu vi hình tròn có tương quan tỷ lệ thuận với bán kính của hình tròn. Khi có một hình tròn bán kính r, đường kính d, ta sẽ có công thức tính chu vi hình tròn như sau :
\(C= 2 * r * \pi= d * \pi\)
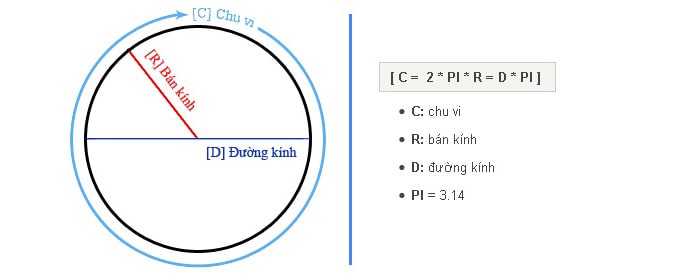
Công thức tính chu vi hình tròn
Có thể phát biểu rằng chu vi hình tròn bằng tích của số Pi và đường kính. Do cùng xuất hiện hằng số Pi trong công thức tính, việc nhầm lẫn giữa công thức tính diện tích hình tròn và công thức tính chu vi hình tròn rất dễ xảy ra. Vì thế bạn cần lưu ý thật kỹ để không bị nhầm lẫn khi cần sử dụng đến hai công thức này.
Vd: Cho hình tròn có đường kính 6cm, tính chu vi hình tròn.
Áp dụng công thức ta có: C = d.π = 6.3,14 = 18,84cm
Diện tích hình tròn được tính bằng bình phương của bán kính r nhân với số Pi, trong đó Pi là hằng số được lấy xấp xỉ bằng 3,14.
Công thức tính diện tích hình tròn được nghiên cứu bởi nhà toán học Hy Lạp cổ đại. Trong quá trình nghiên cứu này, các nhà toán học đã chỉ ra bình phương bán kính hình tròn càng lớn, diện tích của hình tròn càng lớn. Ví dụ ta có một hình tròn có bán kính là r, đường kính là d, ta sẽ có công thức tính diện tích hình tròn như sau:
\(S= r^2 * π = r^2 * 3.14 = \frac{d^2}{ 4} * 3.14 \)
Trong đó:
S: diện tích
r: bán kính
d: đường kính
π: 3.14
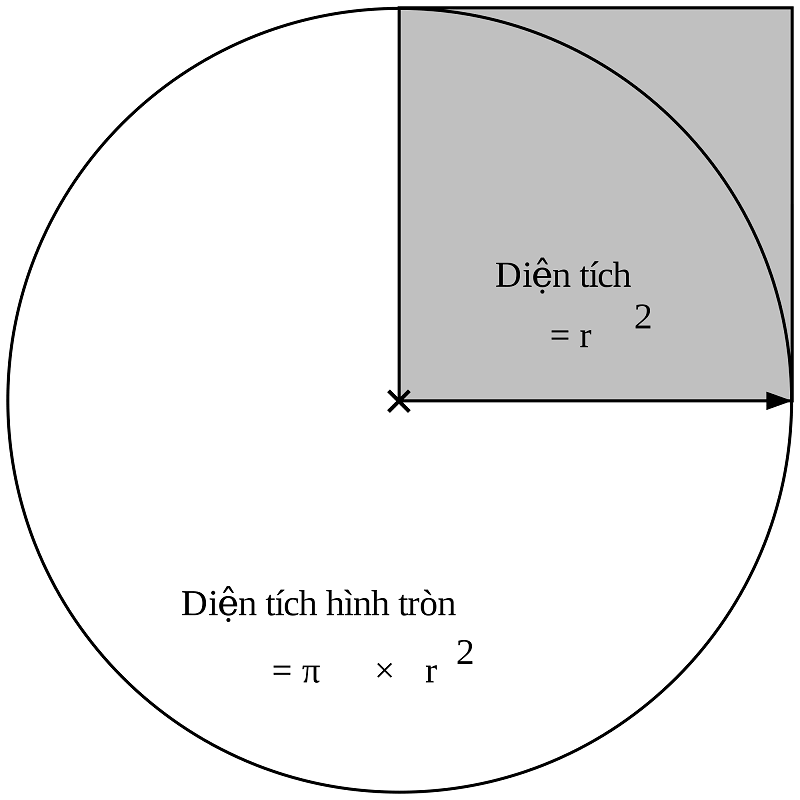
Công thức tính diện tích hình tròn
Các bạn hãy ghi nhớ rằng công thức tính diện tích hình tròn bằng tích của số Pi và bình phương của bán kính. Công thức này tuy đơn giản, nhưng sau một thời gian không sử dụng rất dễ quên hoặc nhầm lẫn. Các bạn hãy lưu ý kỹ để không có những sai sót không đáng có trong quá trình làm bài tập cũng như hướng dẫn cho người khác nhé
Ví dụ: Ta có một hình tròn C có đường kính d=4cm. Tính diện tích hình tròn.
Áp dụng công thức \(S= (\frac{4}{2})^2 .π = 4.3,14\) = 12,56cm2
Ngoài ra bạn còn có thể tính diện tích hình tròn khi biết chu vi theo công thức sau:
\(S = \frac{C^2}{4\pi}\)
Trong đó: C là chu vi hình tròn
VD: Cho hình tròn có chu vi bằng 10cm, tính diện tích hình tròn.
Áp dụng công thức trên ta có: \(S = \frac{C^2}{4\pi} = \frac{10^2}{4*3,14} = 7.96 cm^2\)
Khi học bất cứ một công thức gì, để dễ nhớ điều đầu tiên chúng ta cần nắm rõ chính là bản chất của công thức. Sau khi nắm vững các khái niệm cần liên quan như bán kính, đường kính, tâm, hãy bắt tay vào làm bài tập nhanh chóng để có thể dễ dàng ghi nhớ công thức.
Do đặc thù công thức tính diện tích hình tròn, chu vi hình tròn không dễ nhớ như một số hình đa giác. Nó tồn tại hằng số cố định Pi. Hằng số này có ý nghĩa thực tế như thế nào, ta có thể nghiên cứu ở các chương trình toán học cao cấp sau này. Khi học về các công thức, điều cần thiết bạn phải nhớ là trị giá của số Pi bằng 3.14.
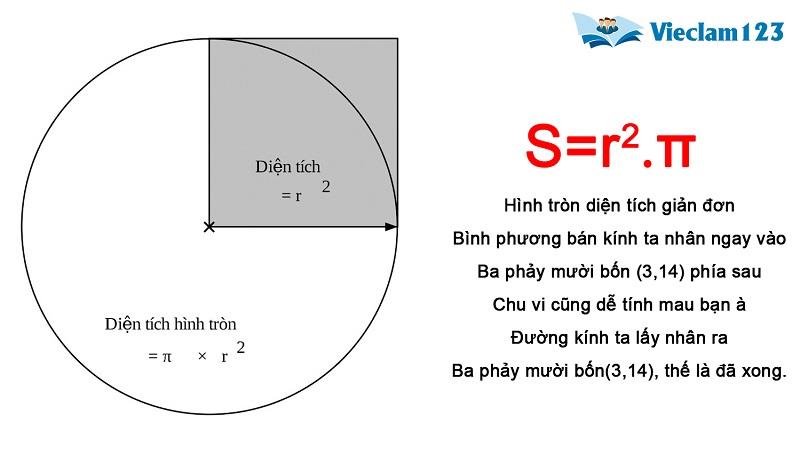
Ngoài việc hiểu bản chất và thực hành nhiều bài tập để có thể dễ dàng ghi nhớ công thức, các bạn cũng có thể tham khảo công thức tính diện tích các hình thông qua những bài thơ được các thầy cô sáng tác. Các công thức toán học khô khan được chuyển thể thành những vần thơ ngộ nghĩnh, dí dỏm sẽ khiến cho các bạn cảm thấy môn học này trở nên gần gũi và dễ học hơn.
Việc dạy toán qua thơ không phải là một vấn đề quá mới đối với các thầy cô giáo và các bậc phụ huynh. Đối với những công thức dễ nhầm như công thức tính diện tích hình tròn, công thức tính chu vi hình tròn, phương pháp này đem lại những kết quả khá tốt.
Tôi xin phép được trích một đoạn thơ vui để ghi nhớ công thức tính diện tích hình tròn, chu vi hình tròn để bạn tham khảo:
Hình tròn diện tích giản đơn
Bình phương bán kính ta nhân ngay vào
Ba phảy mười bốn (3,14) phía sau
Chu vi cũng dễ tính mau bạn à
Đường kính ta lấy nhân ra
Ba phảy mười bốn (3,14), thế là đã xong.
Những vần thơ vui được sáng tác kiểu như trên góp phần rất lớn vào việc tạo cảm hứng để học sinh cảm giác môn toán đỡ căng thẳng hơn và dễ thuộc công thức hơn. Nếu như khó nhớ lại công thức tính diện tích hình tròn,công thức tính chu vi hình tròn quá, bạn có thể tìm một bài thơ có vần kiểu như đoạn thơ trên để học thuộc, vừa giúp giảm bớt nỗi niềm “ sợ Toán”, vừa có thể học bài một cách hiệu quả .
Một số thầy cô còn vận dụng một số cách giải toán bằng thơ. Điều này khiến học sinh vô cùng thích thú và khiến cho nội dung của bài toán trở nên gần gũi hơn với ngôn ngữ, lời ăn tiếng nói hằng ngày. Ngay từ khi đi học, chắc chắn hầu hết chúng ta đều biết tới một vài bài toán được chuyển thể thành thơ, đã trở thành thứ gia vị không thể thiếu để các giờ học toán trở nên sinh động và vui nhộn hơn rất nhiều.
Không ít những học sinh mang trong mình nỗi “sợ Toán”. Các công thức rất nhiều và dài ngoằng khiến cho bạn dễ dàng bị nhầm lẫn từ công thức này sang công thức kia. Lúc này các bài thơ vui có thể được coi như một “cứu cánh” để bạn có thể dễ dàng xem lại bài học và ôn lại kiến thức cho mình. Môn Toán được coi là khô khan, nhưng tìm hiểu sâu về nó, người ta sẽ dễ dàng yêu thích giống yêu một cô gái đang độ mười tám khó chiều, nhưng đã chiều được rồi, thì sẽ có một tình yêu đẹp lắm vậy.
Khi vừa được học chúng ta thấy việc ghi nhớ các công thức tính chu vi hình tròn, diện tích hình tròn không gặp nhiều khó khăn. Nhưng một thời gian không sử dụng lại, đôi khi việc nhầm lẫn xảy ra là điều khó tránh. Như vậy, hãy nhớ một đoạn thơ về cách tích chu vi, diện tích hình tròn, để khi cần, chỉ cần nhẩm qua là có thể nhớ lại bạn nhé.
Nhìn chung lại, để học tốt môn Toán bạn còn cần rất nhiều các yếu tố khác nhau. Mỗi người có thể lựa chọn cho mình một phương pháp học nhưng điều đầu tiên cần là hiểu bạn chất vấn đề, tránh bị hổng kiến thức. Các công thức Toán học là một trong những điều căn cốt bạn cần phải ghi nhớ và tìm hiểu trong quá trình chinh phục môn học này. Trong số đó, đừng bỏ qua những công thức tính đơn giản như công thức tính diện tích hình tròn, công thức tính chu vi hình tròn để ngay từ đầu đã có một nền tảng Toán học thật chắc chắn bạn nhé.
>> Xem thêm bài liên quan:
MỤC LỤC




Chia sẻ