Đăng nhập tài khoản:
Khối đa diện được hiểu là gì? Học sinh cần nắm được những kiến thức gì về nội dụng khối đa diện sẽ có tất cả trong bài viết dưới đây để tiện tham khảo và học tập hơn.
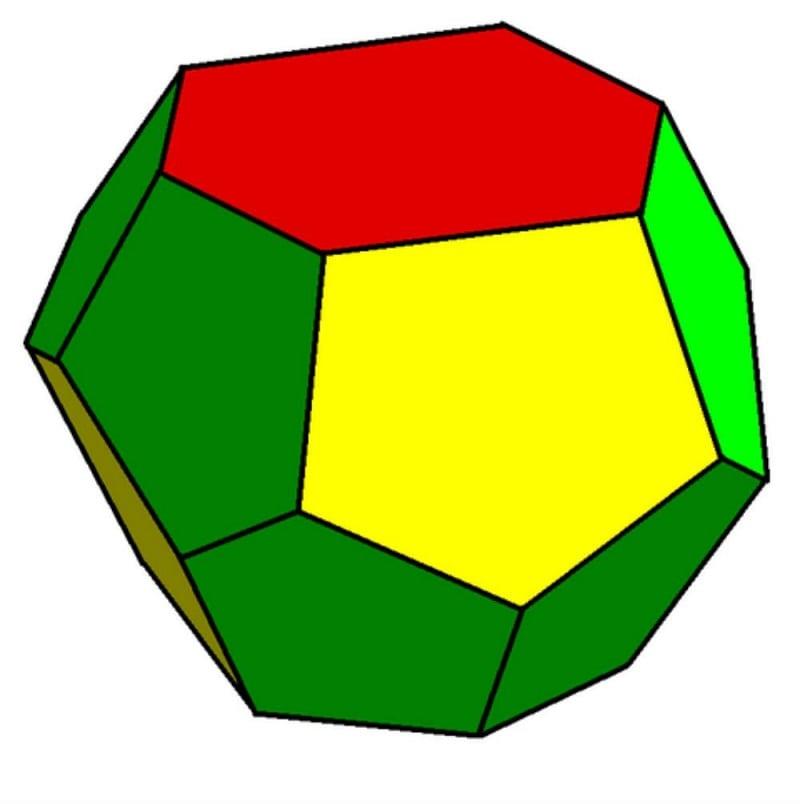
Khối đa diện được định nghĩa là phần không gian giới hạn bởi hình đa diện. Theo đó, ta sẽ chỉ xét hình đa diện và phần trong của nó. Có nghĩa là khối đa diện đó được giới hạn bởi hình đa diện.
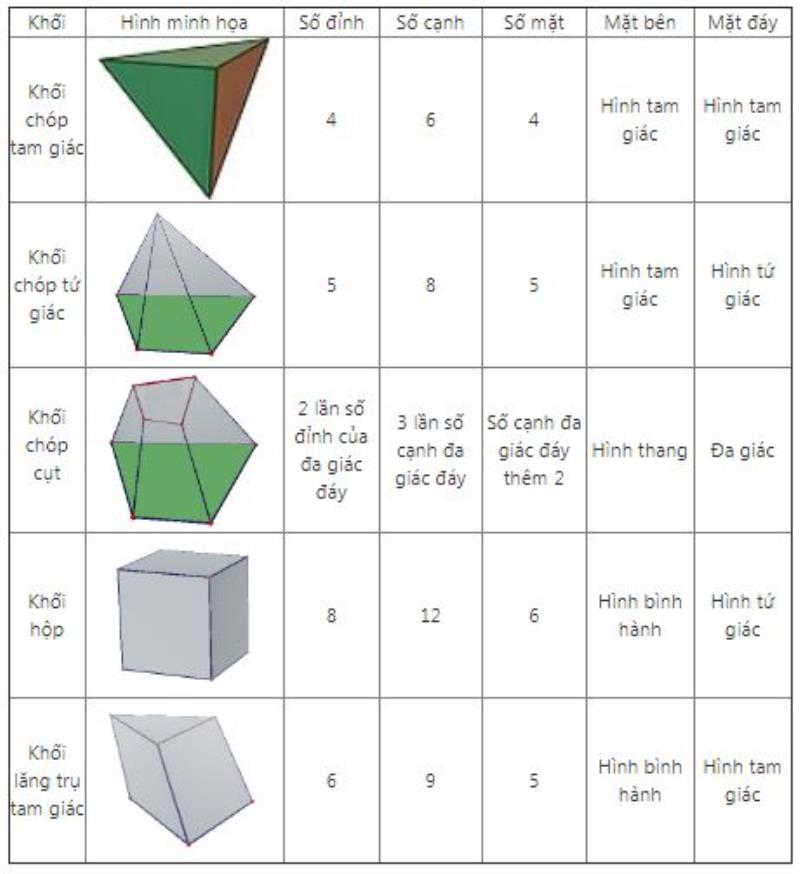
Các khối đa diện thường gặp như khối chóp tam giác, khối chóp tứ giác, khối chóp cụt, khối hộp và khối lăng trụ. Trong đó:
* Khối đa diện lồi có đoạn thẳng nối 2 điểm bất kỳ của nó luôn thuộc chính nó.
* Khối đa diện đều là khối đa diện đều nếu có các tính chất như sau:
+ Mỗi mặt là một đa giác đều gồm n cạnh
+ Mỗi đỉnh là đỉnh chung của đúng m mặt
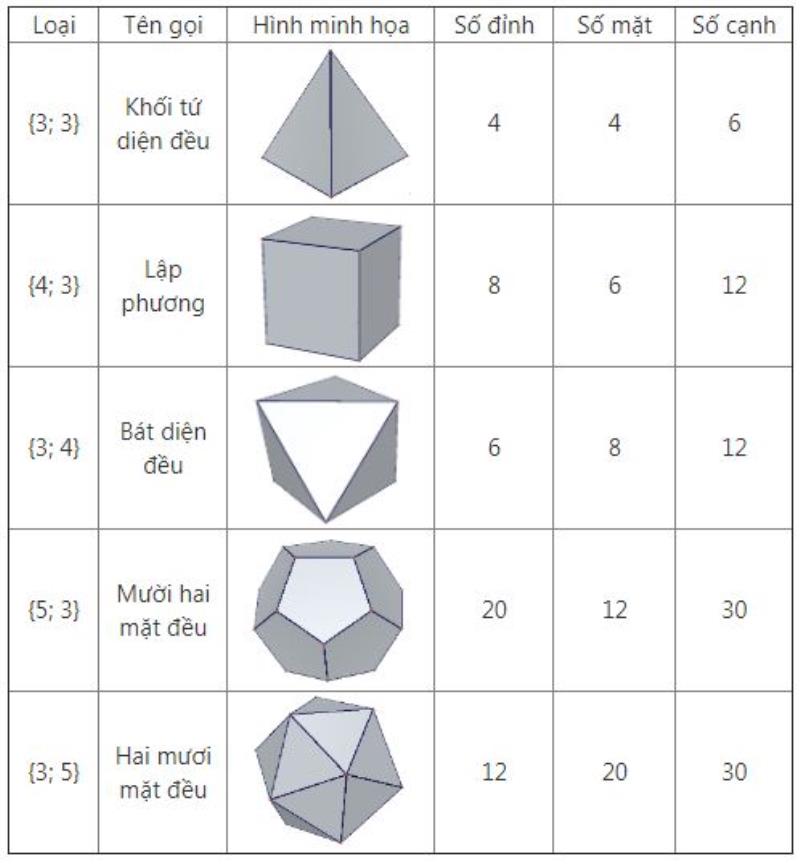
Như vậy, khối đa diện này gọi là khối đa diện lồi loại m;n. Các khối đa diện đều như khối tứ diện đều, hình lập phương, bát diện đều, khối 12 mặt đều, khối 20 mặt đều
Ví dụ: + Đây là các khối đa diện
+ Đây không phải là khối đa diện
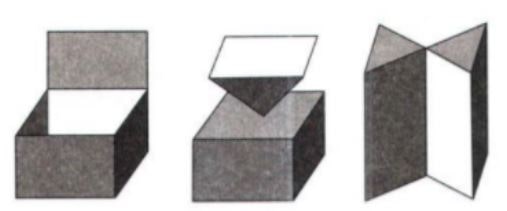
* Khối đa diện được gọi là khối chóp, khối chóp cụt nếu có giới hạn bởi một hình chóp, hình chóp cụt tương ứng.
* Khối đa diện được gọi là khối lăng trụ nếu được giới hạn bởi một hình lăng trụ
* Khối đa diện lồi có 2 điểm bất kỳ nằm trong khối đa diện sẽ tạo thành đoạn thẳng thuộc khối đa diện đó.
Khi học về khối đa diện, học sinh cần nắm được những kiến thức bao gồm:
a. Định nghĩa về đa diện hay hình đa diện. Đó là hình được tạo bởi một số đa giác hữu hạn đáp ứng các điều kiện:
* Hai đa giác phân biệt không hoặc có thể giao nhau, hay có một đỉnh chung, hay một cạnh chung.
* Các đa giác có mỗi cạnh là cạnh chung của chỉ đúng 2 đa giác. Mỗi đa giác đó là một mặt của hình đa diện có các đỉnh, cạnh cũng chính là các đỉnh, cạnh của các đa giác tương ứng.
b. Phần không gian giới hạn bởi hình đa diện nào đó sẽ là khối đa diện.
c. Mỗi đa diện sẽ chia các điểm còn lại của khối thành 2 miền gồm miền trong và miền ngoài của nó không giao nhau. Trong đó, chỉ có miền ngoài sẽ chứa trọn một đường thẳng nào đó. Còn các điểm của miền trong là các điểm trong và các điểm ngoài của đa diện là các điểm thuộc miền ngoài.
* Hợp của hình đa diện và miền trong của nó chính là khối đa diện.
d. Phép dời hình và sự bằng nhau đều có trong khối đa diện. Trong đó:
* Phép biến hình trong không gian là chính là quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất trong không gian.
* Được gọi là phép dời hình nếu phép biến hình trong không gian bảo toàn khoảng cách giữa 2 điểm tùy ý.
* Dù làm liên tiếp nhiều phép dời hình sẽ được 1 phép dời hình.
* Phép dời hình sẽ biến các cạnh, đỉnh, mặt của đa diện này thành của đa diện kia hay biến một đa diện thành một đa diện khác.
* Điểm danh các phép dời hình trong không gian, bao gồm:
+ Phép biến hình biến điểm M thành M’ thỏa mãn điều kiện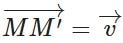 
gọi là phép dời hình tịnh tiến theo vector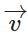 
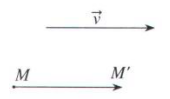
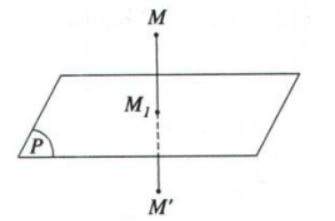
+ Phép biến hình biến mọi điểm thuộc (P) thành chính nó và biến điểm M không thuộc (P) thành điểm M’ thỏa mãn điều kiện (P) là mặt phẳng trung trực của MM’ gọi là phép đối xứng qua mặt phẳng (P). Và (P) sẽ được gọi là mặt phẳng đối xứng của H khi phép đối xứng qua mặt phẳng P biến hình H thành chính nó.
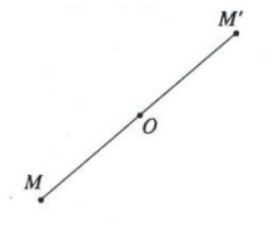
+ Phép đối xứng tâm O xảy ra khi phép biến hình biến điểm O thành chính nó và biến điểm M khác O thành điểm M’ thỏa mãn điều kiện O là trung điểm của MM’. Nếu phép đối xứng tâm O biến hình đa diện thành chính nó thì O sẽ là tâm đối xứng của hình đa diện.
+ Phép biến hình mọi điểm thuộc d thành chính nó và biến điểm M không thuộc d thành M’ thỏa mãn điều kiện d là trung trực của MM’ gọi là phép đối xứng qua đường thẳng d, gọi là phép đối xứng qua trục d. Nếu nó biến hình đa diện thành chính nó, d được gọi là trục đối xứng của nó.
.JPG)
* Nếu một phép dời hình biến hình này thành hình kia sẽ được gọi là hai hình bằng nhau.
* Nếu có các cạnh tương ứng bằng nhau, hai tứ diện được gọi là bằng nhau.
e. Như trong hình vẽ ở trên, nếu H1 và H2 hợp thành khối đa diện (H) khi H1 và H2 không có điểm trong chung, chúng ta chia thành 2 khối đa diện H1 và H2 từ khối đa diện hay ngược lại lắp ghép 2 khối đa diện này với nhau tạo thành khối đa diện H.
f. Mỗi khối đa diện đều phân chia được thành các khối tứ diện.
g. Khối đa diện có tính chất đồng dạng giữa các khối đa diện và phép vị tự trong không gian. Cụ thể:
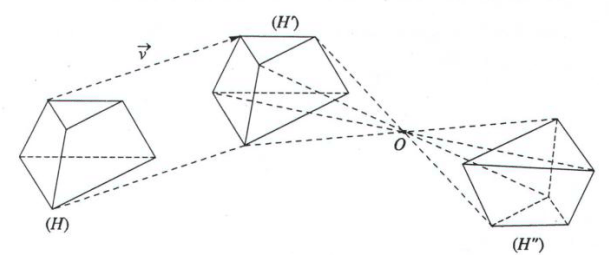
+ Phép biến hình biến điểm M thành điểm M’ thỏa mãn điều kiện (ảnh) chính là phép vị tự tâm O, tỉ số k với k # 0.
+ Nếu phép vị tự biến H thành H1 và H1 bằng H’ thì hình H được gọi là đồng dạng với hình H’ (hình vẽ)
Về phần nội dung này, các bạn học sinh cần chú ý tới các kiến thức sau đây:
* Có thể phân chia thành những khối tứ diện từ một khối đa diện bất kì nào đó. Ví dụ: ảnh
Chia các khối lăng trụ tam giác ABC.A’B’C’ thành 3 khối tứ diện gồm A’.ABC, A’.BCB’, A’.B’C’C hoặc chia khối lăng trụ thành 2 khối chóp C’.ABC và C’.ABB’A’ giống như hình vẽ.
>> Có rất nhiều lớp dạy kèm cần gia sư đang được các bậc phụ huynh đăng mỗi ngày, tham khảo và tìm cho mình một lớp gia sư ngay trên vieclam123.vn
Tiếp theo, chúng ta cùng tham khảo một số bài tập về khối đa diện lồi vận dụng những kiến thức ở trên nhé.
* Câu 1: Hình lập phương có bao nhiêu cạnh, bao nhiêu mặt và số đỉnh?
Trả lời: Với 6 mặt, 8 đỉnh và 12 cạnh, hình lập phương sẽ gồm tổng số là 26.
* Câu 2: Chỉ ra mệnh đề nào sai trong các mệnh đề trên:
Trả lời: Câu D là sai còn các câu còn lại đúng. Vì 2 tứ diện ghép với nhau sẽ tạo thành đa diện lõm. Ví dụ cho 2 đỉnh chạm nhau, các đỉnh còn lại đối xứng qua đỉnh đó.
* Câu 3: Khối hình chóp tam giác có tổng số cạnh là bao nhiêu?
Trả lời: Với 3 cạnh đáy và 3 cạnh bên, khối chóp tam giác có tổng số là 6 cạnh.
* Câu 4: Chọn mệnh đề đúng cho khối chóp n – giác sau đây:
Trả lời: Có mệnh đề C và D đúng, bởi vì:
+ Khối chóp có số cạnh bằng 2n cạnh trong đó có n cạnh bên và n cạnh đáy.
+ Khối chóp có số mặt bằng n + 1 trong đó có một đáy và n mặt bên.
+ Khối chóp có số định bằng n + 1 trong đó có 1 đỉnh chóp và n đỉnh đáy.
+ Khối chóp có số mặt bằng số đỉnh vì đều bằng n + 1
* Câu 5: Khối tứ diện đều có số mặt phẳng đối xứng là bao nhiêu?
Trả lời: Khối tứ diện đều gồm có 6 mặt phẳng đối xứng. Bởi mỗi mặt phẳng đều chứa một cạnh đi qua trung điểm cạnh đối diện chính là một mặt phẳng đối xứng của tứ diện đều.
Tổng hợp các thông tin về khối đa diện ở trên hy vọng đã cung cấp cho bạn những thông tin cần thiết để học và nâng cao hiểu biết của mình.
>> Xem thêm:
Chia sẻ