Diện tích mặt cầu, thể tích hình cầu được học trong chương trình phổ thông mà các em học sinh cần nắm được để có thể theo kịp bài học cũng như áp dụng vào làm bài tập trên lớp, làm bài thi. Sau đây là những thông tin mà bạn cần biết.
MỤC LỤC
Theo wikipedia, mặt cầu có tính đối xứng hoàn hảo của một đối tượng hình học. Xét trong không gian 3D, mặt cầu có tâm điểm O cố định cách đều các điểm khác một khoảng là bán kính không đổi R gọi là quỹ tích. Các bạn có thể phát biểu là: mặt cầu là tập hợp quỹ tích tất cả các điểm cách đều tâm O cố định một khoảng bán kính R.
Vị trí tương đối giữa mặt phẳng và mặt cầu:
.jpg)
Vị trí tương đối của mặt cầu và đường thẳng:
.jpg)
Trong toán học, hình cầu là tất cả phần bên trong của mặt cầu, gồm tập hợp các điểm cách đều một điểm cho trước là tâm.
Nếu mặt cầu chỉ là bề mặt thì hình cầu có không gian 3 chiều. Hình cầu có tâm điểm O cố định cách đều quỹ tích các điểm một khoảng cách bán kính không đổi R.
Chúng ta có thể thấy nhiều vật thể hình cầu trong cuộc sống như quả bóng bi-a, bóng truyền,....
Diện tích được dùng đo độ lớn của bề mặt một vật nên diện tích mặt cầu cũng vậy sẽ gồm những gì có thể nhìn thấy của đối tượng. Cùng tìm hiểu chi tiết hơn về cách tính diện tích của mặt cầu dưới đây.
\(S= 4\pi r^2 = \pi d^2\)
Trong đó:
r là bán kính hình cầu
d là đường kính hình cầu
π lấy bằng sấp sỉ 3,14
Diện tích mặt cầu sẽ bằng 4 Pi nhân với bình phương bán kính hoặc bằng bình phương độ dài đường kính nhân với số Pi.
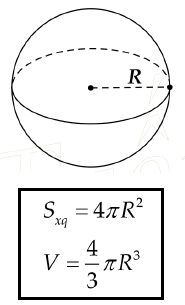
Từ khái niệm về diện tích mặt cầu ở trên, ta có công thức tính như sau: S = 4π^2. r hay πd^2
Trong đó:
• S là ký hiệu diện tích của mặt cầu
• π là ký hiệu của số Pi bằng xấp xỉ 3,14
• d là ký hiệu của đướng kính của mặt cầu, hình cầu.
• r là ký hiệu của bán kính của mặt cầu, hình cầu.
• S là ký hiệu của diện tích của mặt cầu, hình cầu.
• Diện tích của đơn vị đo lường là: m2, cm2…
• Điểm vuông góc và đi qua trung điểm của đoạn thẳng chính là đường trung trực.
• Đường thẳng đi qua tâm đường tròn ngoại tiếp, vuông góc với mặt chứa đa giác đáy gọi là trục đáy
• Đi qua trung điểm của mặt phẳng và vuông góc với đoạn thẳng sẽ là mặt trung trực của đoạn thẳng.
Như vậy, diện tích của mặt cầu ngoại tiếp có công thức như ở trên. Để tính được diện tích của mặt cầu ngoại tiếp, bạn cần biết bán kính mặt cầu và tâm của mặt cầu tương ứng với các hình học khác như hình lăng trụ đứng, hình chóp, hình chữ nhật và hình lập phương.
Để tính diện tích mặt cầu hay hình cầu, bạn áp dụng công thức trên khi biết tất cả các dữ liệu như bán kính hay đường kính. Bạn thay số vào công thức và thực hiện phép tính. Ngoài công thức chung này, chúng ta có những cách tính diện tích của mặt cầu đặc biệt sẽ có ở phần tiếp theo sau đây.
Ở trên chúng ta đã có khái niệm về hình cầu. Hãy tham khảo chi tiết về tính thể tích hình cầu nhé.
Về cơ bản, hình cầu và mặt cầu giống nhau về nghĩa và chỉ có sự khác nhau về hình học khi mà hình cầu có không gian 3 chiều với mỗi điểm nằm trên bề mặt sẽ có khoảng cách đến tâm bằng nhau đó là bán kính R, còn mặt cầu chỉ là bề mặt 2 chiều.
Trong cuộc sống có nhiều đồ vật có hình cầu như quả địa cầu, quả bóng… Muốn tính thể tích hình cầu, ta sẽ phải biết hoặc tìm độ dài bán kính của hình sau đó, áp dụng công thức tính thể tích hình cầu là sẽ ra kết quả đơn giản:
V = ⁴⁄₃πr³
Trong đó:
• V: ký hiệu thể tích hình cầu
• R: bán kính của khối cầu
• π là ký hiệu số Pi = 3,14
Sau đây là các bước tính thể tích hình cầu dành cho bạn:
Viết công thức tính thể tích hình cầu
Khi nhận đề bài tính thể tích hình cầu, đầu tiên, bạn cần viết ra công thức tính thể tích đã học sau đó, bạn xem xét xem dữ liệu bán kính của hình cầu đã cho hay chưa. Nếu đã cho, bạn thay số vào công thức và tính ra kết quả là thể tích hình cầu cần tìm.
Nếu đề bài chưa cho độ dài bán kính, bạn cần tìm bán kính trước sau đó mới thay vào và áp dụng công thức tính thể tích hình cầu nhé.
Tìm bán kính của hình cầu
Bạn dựa vào dữ liệu mà đề bài cho như số đo đường kính. Muốn tìm bán kính, bạn lấy đường kính chia cho 2 sẽ ra bán kính cần tìm. Nếu cho diện tích mặt cầu S, bạn tìm bán kính dựa vào công thức tính diện tích mặt cầu để tính.
Tính lũy thừa bậc 3 của bán kính
Tìm ra bán kính, muốn tính lũy thừa bậc 3 của nó, bạn đem bán kính nhân với với chính nó 3 lần hoặc nâng lên số mũ 3. Sau đó, áp dụng công thức tính thể tích hình cầu ở trên, thay số vào và tính phép tính. Lưu ý, thể tích hình cầu có đơn vị là thể tích ví dụ cm3, dm3... Ví dụ, bán kính là 3cm thì lũy thừa bậc 3 lên ta có 33 hay 3 x 3 x 3 = 8
Nhân lũy thừa bậc 3 của bán kính với 4/3
Thay r3 vào công thức tính thể tích V = ⁴⁄₃πr³ tính ra kết quả chính là thể tích hình cầu mà bạn đang cần tìm.
Những điều cần lưu ý khi tính thể tích hình cầu
• Đơn vị đo của đáp án luôn là đơn vị khối ví dụ cm3, dm3...
• Cùng đơn vị đo. Nếu không cùng đơn vị đó, bạn phải quy đổi về cùng một đơn vị đo là m, dm, cm…
• Muốn tính thể tích từng phần của hình cầu như một phần tư thể tích hay ½ thể tích, bạn cần tính thể tích toàn phần sao đó nhân với phân số tương ứng số phần mà bạn cần tìm. Ví dụ nếu thể tích toàn phần của hình cầu là 8 thì thể tích ½ sẽ bằng 8 nhân với ½ bằng 4.
S mặt cầu = 4 π.R^2 hoặc: S mặt cầu = π. d^2
Đây là 2 công thức mà bạn có thể áp dụng tính diện tích mặt cầu trong các bài tập. Như vậy, khi biết đơn vị đo lường của bán kính hay biết đường kính, bạn đều có thể tính diện tích mặt cầu được.
Bài tập 1: Với các bán kính nối từ tâm O dưới đây, bạn tính diện tích mặt cầu:
a. 9m
b. 1,5dm
c. 2cm
d. 15cm
Bài giải: Bạn đã biết bán kinh của mặt cầu. Soi vào công thức Smặt cầu = 4 π.R^2, bạn đã có đủ yếu tố để tính diện tích của mặt cầu này bằng cách thay số vào công thức trên, ta được:
a. S = 4 x 3,14 x 9^2 = 1017.36 m2
b. S = 4 x 3,14 x 1,5^2 = 28.26 dm2
c. S = 4 x 3,14 x 2^2 = 50.24 cm2
d. S = 4 x 3,14 x 15^2 = 2826 cm2
Bài tập 2: Với đường kính có độ dài cho như dưới đây, tính diện tích mặt cầu:
a. 2,5cm
b. 10cm
c. 1/2cm
d. 4,5cm
Bài giải: Đề bài đã cho độ dài đường kính cụ thể, do đó ta hoàn toàn có thể tính diện tích mặt cầu theo công thức: Smặt cầu = π. d2
a. S = 3,14 x 2,5^2 = 19,625 cm2
b. S = 3,14 x 10^2 = 314 cm2
c. S = 3,14 x 1/4 = 0,785 cm2
d. S = 3,14 x 4,5^2 = 63,585 cm2
Đây là dạng bài tính diện tích mặt cầu một phép tính khá đơn giản mà học sinh chỉ cần thay số vào đại lượng tương ứng và thực hiện phép tính sẽ cho ra kết quả diện tích của mặt cầu.

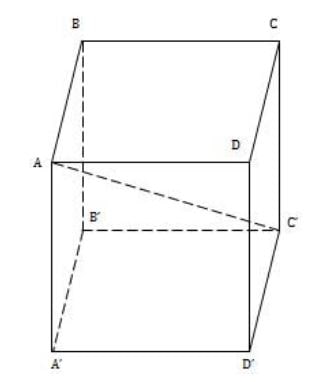
Bài tập: Đề bài yêu cầu tính thể tích khối cầu của hình lập phương ABCD.A'B'C'D' có độ dài các cạnh là a. Tính thể tích khối cầu như sau:
a. Tính thể tích khối cầu ngoại tiếp hình lập phương
b, Tính thể tích khối cầu nội tiếp hình lập phương
Bài giải:

Trên đây là những kiến thức về diện tích mặt cầu, thể tích hình cầu mà các bạn học sinh cần nắm chắc kiến thức, tính chất cũng như luyện tập làm bài tập để áp dụng lý thuyết vào làm bài tập thành thạo. Nắm chắc kiến thức và luyện tập làm bài tập là những yếu tố giúp các em học sinh đạt được điểm tốt.
Hy vọng những thông tin về diện tích mặt cầu, thể tích hình cầu ở trên sẽ giúp ích cho bạn trong quá trình học tập của mình. Truy cập vieclam123.vn để cập nhật thêm nhiều bài học khác.
>> Tham khảo thêm:
MỤC LỤC




Chia sẻ