Toán học là môn học quan trọng và cần thiết trong chương trình học, tham khảo bài viết để biết được công thức cũng như cách học của 7 hằng đẳng thức đáng nhớ.
MỤC LỤC
Các hằng đẳng thức đáng nhớ là một phần kiến thức quan trọng được học ở bậc trung học, việc ghi nhớ và áp dụng 7 hằng đẳng thức đáng nhớ là cần thiết. Hãy cùng vieclam123.vn tìm hiểu sâu hơn về hẳng đẳng thức qua bài viết sau đây.
Bảy hằng đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình môn toán THCS, các bạn được tiếp xúc đầu tiên ngay từ khi bắt đầu lên lớp 8 và khi lên các lớp cao hơn thì bảy đẳng thức đáng nhớ được áp dụng trong các bài toán nâng cao nhiều hơn, và theo các bạn suốt quãng đường học tập. Bảy đẳng thức đáng nhớ giống như cái tên gọi của nó, “đáng nhớ” ở đây và thể hiện vai trò của nó trong việc tiếp thu kiến thức của các bạn trẻ, hằng đẳng thức là công cụ đem lại nhiều lợi ích khi áp dụng vào môn toán ở chương trình học tập.

+ Khi đã nắm chắc chắn cách dùng cũng như hiểu bản chất của bảy hằng đẳng thức đang nhớ thì việc vận dụng tốt 7 hằng đẳng thức đáng nhớ để giải toán là điều không khó, học sinh sẽ tiết kiệm được thời gian, công sức trong việc giải bài tập, cách giải sẽ dễ hiểu và hạn chế nhiều sai sót khi biến đổi công thức.
+ 7 hằng đẳng thức đáng nhớ là công cụ không thể thiếu trong vốn kiến thức của học sinh, nhờ việc học các hằng đẳng thức giúp các bạn học sinh rèn được các kỹ năng quan sát, nhận xét cũng như sự tỉ mỉ trong khi phân tích các vấn đề trong toán học cũng như rèn luyện các kỹ năng cẩn thận cả trong những tình huống đời thường.
+ Khi vận dụng các đẳng thức tốt, giúp kết quả học tập của các bạn được nâng cao, các bạn sẽ thấy thích thú, đam mê và có tinh thần hứng thú trong việc học toán, việc suy nghĩ cách giải bài toán ở những bài tập khó phải áp dụng hằng đẳng thức để phân tích giúp các bạn tăng sự tư duy, tăng sự phát triển não bộ, và việc học các đẳng thức đáng nhớ góp phần trong việc phát triển trí tuệ và sự thông minh của trẻ ngay từ nhỏ.
“Bảy hằng đẳng thức đáng nhớ” là kiến thức bắt buộc phải ghi nhớ khi học môn toán. 7 hằng đẳng thức được thể hiện qua ký hiệu các chứ cái và đã được chứng minh sự đúng đắn của mỗi đẳng thức. Những hằng đẳng thức đáng nhớ là một phần trong những hằng đẳng thức đại số cơ bản, vì thế ngoài 7 hằng đẳng thức bạn cũng nên ghi nhớ thêm một vài đẳng thức thông dụng khác.

Công thức bảy hằng đẳng thức đáng nhớ bạn cần phải học thuộc:
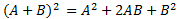
Giải thích công thức bằng lời : Bình phương của một tổng bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất nhân với số thứ hai, cộng với bình phương của số thứ hai
Ví dụ :

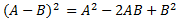
Giải thích công thức bằng lời : Bình phương của một hiệu bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất nhân số thứ hai sau đó cộng bình phương với số thứ hai.
Ví dụ :

2.3. Hiệu hai bình phương
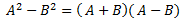
Giải thích : Hiệu hai bình phương của hai số bằng tổng hai số đó nhân với hiệu hai số đó.
Ví dụ :
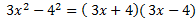
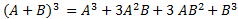
Giải thích bằng lời : Lập phương của một tổng hai số bằng lập phương của số thứ nhất cộng với ba lần tích bình phương số thứ nhất nhân số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai cộng với lập phương số thứ hai.
Ví dụ:
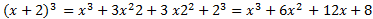
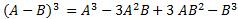
Giải thích bằng lời : Lập phương của một hiệu hai số bằng lập phương của số thứ nhất trừ đi ba lần tích bình phương của số thứ nhất nhân với số thứ hai cộng với ba lần tích số thứ nhất nhân với bình phương số thứ hai trừ đi lập phương số thứ hai
Ví dụ:
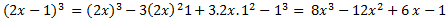
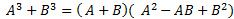
Giải thích bằng lời : Tổng của hai lập phương hai số bằng tổng của hai số đó nhân với bình phương thiếu của hiệu hai số đó
Ví dụ:
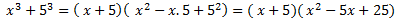
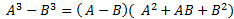
Giải thích bằng lời : Hiệu của hai lập phương của hai số bằng hiệu hai số đó nhân với bình phương thiếu của tổng của hai số đó.
Ví dụ:
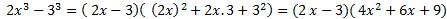
Với A,B có thể là các số hoặc ở dạng chữ (đơn thức, đa thức) hay A,B là các biểu thức bất kỳ, áp dụng các hằng đẳng thức vào bài tập cụ thể thì điều kiện của A, B cần có để thực hiện làm bài tập dưới đây:

+ Biến đổi các hằng đẳng thức chủ yếu là cách biến đổi từ tổng, hiệu thành tích giữa các số, kỹ năng phân tích đa thức thành nhân tử phải thành thạo thì áp dụng các hằng đẳng thức mới rõ ràng và chính xác được.
+ Để hiểu rõ về bản chất sử dụng hằng đẳng, khi áp dụng vào bài toán, học sinh có thể chứng minh sự tồn tại của hằng đẳng thức là đúng đắn bằng cách chuyển đổi ngược lại, sử dụng các hằng đẳng liên quan vào việc chứng minh bài toán.
+ Trong khi sử dụng hằng đẳng thức trong phân thức đại số, học sinh cần lưu ý rằng sẽ có nhiều hình thức biến dạng của công thức do tính chất mỗi bài toán nhưng bản chất vẫn là những công thức ở trên, chỉ là sự biến đổi qua lại để phù hợp trong việc tính toán.
Ví dụ :
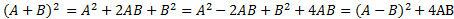
Hằng đẳng thức mở rộng với hàm bậc 2



Hằng đẳng thức mở rộng với hàm bậc 3









Hằng đẳng thức dạng tổng quát


* Với n là số lẻ thuộc N (tập hợp số tự nhiên)
Nhị thức Newton

Với a,b thuộc tập hợp số thực (R), n thuộc tập hợp số tự nhiên dương (N*)
Hằng đẳng thức về căn bậc 2
\(\sqrt{A} = |A|\)
Hằng đẳng thức bắc cầu (tính chất bắc cầu)
Nếu a=c và b=c thì a=b
Từ tính chất bắc cầu ta có thể mở rộng để giải bài tập:
>> Làm đề thi Toeic cùng hệ thống thi thử Toeic online miễn phí đề thật IIG của vieclam123.vn để nâng cao khả năng Toeic của bản thân một cách nhanh chóng.
Một số phương pháp nhằm giúp các bạn học sinh có thể ghi nhớ bảy hằng đẳng thức một cách hiệu quả nhất
Bất kỳ kiến thức nào dù ở lĩnh vực nào, đặc biệt là các hằng đẳng thức đáng nhớ, nếu muốn ghi nhớ kiến thức đó như là tài sản vốn có của mình thì học sinh phải thường xuyên vận dụng nó hàng ngày, sự rèn luyện sẽ hình thành cho các bạn những thói quen tốt. Học sinh nên học các đẳng thức mỗi ngày, vận dụng chúng thành thạo vào những bài toán trước tiên là đơn giản sau đó mới phức tạp dần lên. Vận dụng thường xuyên còn giúp các bạn rèn được tính kiên trì, tìm tòi cũng như khám khá được công thức mới mà mình chưa biết một cách thích thú. Không có tri thức nào là mãi mãi nếu các bạn không thường xuyên trau dồi nó, cũng như phát triển nó. Hằng đẳng thức như một kiến thức vốn có mà khoa học đã chứng minh cụ thể tính đúng đắn của nó, việc học sinh làm là dùng nó theo cách tiếp thu của bản thân một cách chính xác, vì nó phục vụ rất nhiều trong quá trình làm bài của các bạn, đặc biệt những bài tập khó, những bài tập đánh giá sự thông minh của học sinh trong các kỳ thi hay bài kiểm tra.
Bài hát về 7 Hằng đẳng thức (Sau tất cả cover by Nhật Anh)
Sự phát triển của tri thức cũng như khoa học công nghệ, việc sáng tác các bài hát trong việc ghi nhớ kiến thức ngày càng nâng cao. Những bài hát hài hước, vui nhộn liên quan đến kiến thức học, giúp não bộ của học sinh tiếp thu tốt hơn, một minh chứng cụ thể là 7 hằng đẳng thức đáng nhớ thay vì khó học với các con số, người ta thay chúng bằng phiên bản qua bài hát “sau tất cả” với nội dung liên quan đến các hằng đẳng thức, thu hút được sự chú ý cũng như sự thích thú của nhiều bạn trẻ, phục vụ trong việc nhớ kiến thức lâu dài.
Những kiến thức về 7 hằng đẳng thức đáng nhớ và các hệ thức liên quan được áp dụng rất nhiều trong các bài kiểm tra và bài thi. Các bạn hãy ghi nhớ những kiến thức mà vieclam123.vn chia sẻ để học tập tốt hơn nhé!
>> Tham khảo thêm:
MỤC LỤC




Chia sẻ